CURTOSE
Curtose é o grau de achatamento da distribuição ou o quanto uma curva de
frequência será achatada em relação a uma curva normal de referência.
Para o cálculo do
grau de curtose de uma distribuição utiliza-se o coeficiente de curtose (ou
coeficiente percentílico de curtose), definido como:
Em que Q3 e Q1 são
o terceiro e primeiro quartil P90 e P10 são o décimo e nonagésimo percentis.
Quanto à curtose, a
distribuição pode ser:
A. Mesocúrtica –
normal. Nem achatada, nem alongada. (C = 0,263)
Figura 1.8 - Curtose - Mesocúrtica
Fonte: Elaborada pelos autores.
B. Platicúrtica –
achatada. (C > 0,263)
Figura 1.9 - Curtose - Platicúrtica
Fonte: Elaborada pelos autores.
C. Leptocúrtica
– alongada. (C < 0,263
Figura 1.10 - Curtose - Leptocúrtica
Fonte: Elaborada pelos autores.
Nessa primeira
unidade foi abordada a estatística descritiva, que é aquela que tem por finalidade
descrever e sumarizar um conjunto de dados relativos a uma população (universo)
ou a uma amostra.
Iniciamos a unidade
com definições das variáveis de estudo e, em seguida, estudamos as técnicas de
amostragem de dados, onde aprendemos as seguintes técnicas de amostragem:
simples, estratificada e sistemática. Em seguida, passamos a construir tabelas
de distribuição de frequência, com objetivo de tabular os dados coletados.
Em um segundo
momento desta unidade, aprendemos as técnicas de medidas de posição – média,
moda, mediana e medidas de separatrizes. Essas medidas de posição são
importantes, pois descrevem a posição do conjunto de dados e ainda possibilitam
determinar se um valor está entre o maior e o menor valor de uma série
estatística, ou ainda se está localizado no centro do conjunto.
Finalizamos a
unidade com as medidas de dispersão (ou variabilidade), onde estudados: amplitude,
variância, desvio-padrão, coeficiente de variação e as medidas de assimetria e
curtose. As medidas de dispersão foram importantes no nosso estudo, pois
serviram para avaliar o quanto os dados estavam semelhantes ou o quanto os
dados estavam distantes do valor central.
SAIBA MAIS
O documentário O
Prazer da Estatística – The Joy of Statistics – leva os espectadores a uma
viagem por meio do maravilhoso mundo da estatística para explorar o notável
poder que tem de mudar a nossa compreensão do mundo. Este documentário é
apresentado pelo Professor Hans Rosling, cuja visão aberta, de expansão da
mente e engraçadas palestras on-line têm feito dele uma lenda internacional na
internet. Rosling é um homem que se deleita no glorioso mundo das estatísticas,
e aqui ele explora sua história, como elas funcionam matematicamente e como
elas podem ser usadas atualmente no computador para ver o mundo como ele
realmente é, e não apenas como o imaginamos ser.
O documentário
encontra-se disponível no YOUTUBE, no link a seguir em: http://www.youtube.com/watch?v=xLr68J2yDJ8 . Acesso em:
18/02/2018.
ATIVIDADES
1) Em uma
amostragem sistemática, de tamanho 50, de uma população de 2000 elementos, o
primeiro elemento selecionado é o 16. Os dois elementos seguintes a serem
escolhidos são:
a. 32 e 48
b. 50 e 66
c. 50 e 100
d. 56 e 96
e. 56 e 106
2) (CESGRANRIO) Uma
distribuição de frequência incompleta é apresentada na tabela a seguir.
Os valores de x e y
são, respectivamente, iguais a:
a. 130 e 0%.
b. 130 e 10%.
c. 150 e 35%.
d. 200 e 35%.
e. 200 e 50%.
3) (CESGRANRIO) O
supervisor de uma fábrica anotou o tempo de utilização de uma máquina durante 5
dias. Os dados estão na tabela a seguir.
Em média, quantas
horas diárias essa máquina foi utilizada nesses 5 dias?
a. 5
b. 6
c. 7
d. 8
e. 9
4) (CESGRANRIO) O registro
mensal de mercadorias com peso maior do que 0,5 kg despachadas por uma
transportadora, nos últimos 8 meses, foi: 7, 33, 15, 21, 11, 35, 7 e 7. A
mediana associada aos dados anteriores é:
a. 7
b. 13
c. 15
d. 16
e. 17
5) (CESGRANRIO)
Considere o seguinte conjunto: {15; 17; 21; 25; 25; 29; 33; 35}. A média, a
mediana e a moda desse conjunto de dados são, respectivamente:
a. 1, 2 e 3.
b. 5, 7 e 9.
c. 7, 9 e 5.
d. 25, 25 e 25.
e. 25, 27 e 29.
INDICAÇÃO DE LEITURA
Nome do livro:
Estatística Fácil
Editora: Saraiva
Autor: Antônio
Arnot Crespo
Ano: 2009 – 19ª
edição
ISBN:
978-85-02-081106-2
Comentário: Este
livro nos apresenta o conteúdo da estatística de forma fácil e com muitos exemplos
de aplicações, com abundância de situações práticas. Nele estão contidos temas
como: estatística descritiva, tabelas, distribuição de frequências, gráficos,
probabilidades e suas distribuições e finaliza os estudos com a correlação e
regressão linear. No seu final, apresenta uma revisão de matemática que poderá
auxiliá-lo(a) na resolução de exercícios.
ANEXO
Tabela de Números Aleatórios
Figura
1.11 - Tabela de números aleatórios
Fonte: Crespo, 2009, p. 217.
Probabilidades
INTRODUÇÃO
Athanasios
Papoulis, um engenheiro e matemático grego, o qual escreveu o livro Probability,
Random Variables, and Stochastic Processes, que é usado nas principais
escolas de
engenharia do mundo, disse:
As teorias científicas lidam com conceitos, não com
a realidade. Embora elas sejam formuladas para corresponder à realidade, esta
correspondência é aproximada e a justificativa para todas as conclusões
teóricas é baseada em alguma forma de raciocínio indutivo (1991, p. 02).
Desde o período dos
primeiros estudos matemáticos de probabilidades até a metade do século XX, surgiram várias aplicações da
Teoria das Probabilidades, aplicações que chamamos de clássicas, tais como:
cálculo associados aos seguros de vida (cálculos atuariais); cálculos
referentes aos estudos de incidência de doenças infecciosas e o efeito da vacinação,
como o caso recente da gripe H1N1 (estudos demográficos); teoria de jogos como
loteria, carteados etc. Todas essas teorias estão baseadas em probabilidades.
Há registros
históricos de censos, para fins de alistamento militar e de coleta de impostos,
realizados há mais de 4.000 anos, como é o caso do censo do imperador Yao na
China.
Em todo esse tempo,
a estatística era usada meramente para o trabalho de exibição e síntese dos
dados referentes colhidos pelo censo, ou seja, tratava-se da Estatística Descritiva,
a qual não envolvia nenhum trabalho probabilístico, pois todos os objetos do universo
envolvidos (a população) eram apenas observados e medidos.
A primeira pessoa a
pensar em medir/observar uma amostra e, a partir da análise probabilística, estender
os resultados da amostra para todo o universo, foi Adolphe Quételet no ano de
1850. A partir dele, rapidamente surgiu a ideia de dar uma consistência mais rigorosa
para o método científico, a partir de uma fundamentação probabilista para as etapas
da coleta e análise indutiva de dados científicos e essa ideia é usada até hoje
para tomada de decisões.
Nesta unidade,
abordaremos os conceitos básicos de probabilidade e os casos de distribuição binomial
e normal.
PROBABILIDADE
A teoria das
probabilidades nos permite construir modelos matemáticos que explicam um grande
número de fenômenos coletivos ou individuais e fornecem informações para tomada
de decisões.
Para melhor
entender essa unidade, vamos relembrar alguns conceitos básicos:
A. Experimento: É
qualquer processo que permite a um pesquisador fazer observação. Exemplos: o
preço das ações um uma bolsa de valores, o número de funcionários de uma
empresa, o preço das taxas de juro no cheque especial, lançamento de um dado
etc.
B. Experimento
Aleatório: São fenômenos que, mesmo quando repetidos várias vezes, sob
condições semelhantes, apresentam resultados imprevisíveis. O resultado final
sempre depende do acaso.
C. Evento: É
qualquer conjunto de resultados de um experimento. O evento pode ser simples ou
composto. Um evento simples é aquele em que um resultado não pode ser
decomposto em componentes mais simples. Já o evento composto é aquele
que pode ser decomposto em dois ou mais eventos simples. Um evento estatístico
é um conjunto, para o qual definimos as seguintes operações:
D. Espaço
Amostral: Consiste de todos os eventos simples possíveis de um experimento,
ou seja, o espaço amostral consiste em todos os resultados de um experimento
que não pode mais ser decomposto. Exemplo: no lançamento de um dado, o espaço
amostral é formado por seis eventos, a saber, S = {1, 2, 3, 4, 5, 6}.
Se considerarmos S
como espaço amostral e E como evento: assim, qualquer que seja
E, se E ⊂ S (E está contido em S), então E é um evento de S.
Daí:
Se E = S, E é
chamado de evento certo.
Se E ⊂ S e E é um conjunto unitário, E é chamado de evento
elementar.
Se E = ∅, E é chamado de evento impossível.
Chamamos de probabilidade de um evento E (E ⊂ S) o número real P(E)
tal que:
Em que n (E) é o
número de elementos do evento E e n(S) é o número de elementos do espaço
amostral.
Exemplo 1: Ao lançarmos um dado, qual a probabilidade de obter um número par?
Solução: Para a
situação do lançamento de dado temos que o espaço amostral é S = { 1,2,3,4,5,6
} , o qual possui 6 elementos. O evento, que é a ocorrência de número par, é o
conjunto E = { 2,4,6 }, que possui 3 elementos. Assim:
Exemplo 2 (CESGRANRIO): Em uma caixa são colocados vários cartões, alguns amarelos,
alguns verdes e os restantes pretos. Sabe-se que 50% dos cartões são pretos, e que,
para cada três cartões verdes, há cinco cartões pretos. Retirando-se, ao acaso,
um desses cartões, a probabilidade de que este seja amarelo é de:
A. 10%
B. 15%
C. 20%
D. 25%
E. 40%
Solução: Digamos
que sejam colocados 100 cartões na caixa, logo pretos, que 50% do total, ou 50
cartões, são pretos. Como a relação de pretos e verdes é que para cada 3 verdes
há 5 pretos, então 50 pretos corresponderão a 30 verdes e, por conseguinte, amarelos
serão 20. Daí,
Exemplo 3 (CESGRANRIO): Dois dados comuns, honestos, foram lançados
simultaneamente.
Sabe-se que a
diferença entre o maior resultado e o menor é igual a um. Qual é a
probabilidade de que a soma dos resultados seja igual a sete?
A. 1/3
B. ¼
C. 1/5
D. 1/6
E. 1/7
Solução: No
lançamento de dados, os possíveis resultados obtidos são {(1,1), (1,2), (1,3),
(1,4), (1,5), (1,6), (2,1), (2,2), (2,3), (2,4), (2,5), (2,6), (3,1), (3,2),
(3,3), (3,4), (3,5), (3,6), (4,1), (4,2), (4,3), (4,4), (4,5), (4,6), (5,1),
(5,2), (5,3), (5,4), (5,5), (5,6), (6,1), (6,2), (6,3), (6,4), (6,5), (6,6)}.
Vamos assinalar os resultados cuja diferença seja um. Assim, teremos 5
resultados favoráveis à diferença um. Daí, a probabilidade de que a soma dos resultados
seja igual a sete é:
Exemplo 4 (CESGRANRIO): Foi observado que uma loja de departamentos recebe, por hora,
cerca de 250 clientes. Destes:
I. 120 dirigem-se
ao setor de vestuário.
II. 90 ao setor de
cosméticos.
III. 80 ao setor
cinevídeo.
IV. 50 dirigem-se
aos setores de vestuário e de cosméticos.
V. 30 aos setores
de cosméticos e de cinevídeo.
VI. 30 aos setores
de vestuário e cinevídeo.
Observou-se, ainda,
que 50 clientes se dirigem a outros setores que não vestuário ou cosméticos ou
cinevídeo. Qual a probabilidade de um cliente entrar nessa loja de
departamentos e se dirigir aos setores de vestuário, de cosméticos e de
cinevídeo?
A. 0,08
B. 0,20
C. 0,36
D. 0,48
E. 0,80
Solução:
Primeiramente, montamos o Diagrama de Venn, como ilustrado a seguir. Assim, e
em seguida, determinamos o valor de x.
Figura 2.1 - Diagrama de Venn 1
Fonte: Elaborada pelos autores.
Daí, (40 + x) + (20
+ x) + (10 +x) + (30 - x) + 50 - x) +30 - x) + x = 200
180 + x = 200
x = 20
Assim, o diagrama
de Venn fica como mostrado a seguir:
Figura 2.2 -
Diagrama de Venn 2 Fonte: Elaborada pelos autores.
Se P(A) é a
probabilidade de um cliente entrar nessa loja de departamentos e se dirigir aos
setores de vestuário, de cosméticos e de cinevídeo, então segue que:
Vejamos, agora,
como proceder ao cálculo da probabilidade para o caso em que os eventos são
independentes. Dizemos que dois eventos são independentes quando a realização
(ou não realização) de um dos eventos não afeta a probabilidade da realização
do outro e vice-versa. Por exemplo, quando lançamos dois dados não viciados, o
resultado obtido por um independe do resultado obtido no outro. No caso de
eventos independentes, a probabilidade de que eles se realizem simultaneamente
é igual ao produto das probabilidades de realização de cada evento.
Exemplo 5: Dois dados comuns, honestos, foram lançados simultaneamente. Qual a
probabilidade de se obter o número 2 no primeiro dado e o número 5 no segundo
dado?
Solução: Note que
se trata de eventos independentes. Assim, a probabilidade de obtermos o número
2 na primeira jogada é 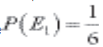 e a probabilidade de se obter o número 5 no segundo dado
é igual a
e a probabilidade de se obter o número 5 no segundo dado
é igual a 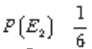 . Logo, a probabilidade de obtermos, simultaneamente, 2 na primeira
jogada e 5 na segunda jogada é:
. Logo, a probabilidade de obtermos, simultaneamente, 2 na primeira
jogada e 5 na segunda jogada é:
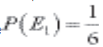 e a probabilidade de se obter o número 5 no segundo dado
é igual a
e a probabilidade de se obter o número 5 no segundo dado
é igual a 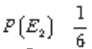 . Logo, a probabilidade de obtermos, simultaneamente, 2 na primeira
jogada e 5 na segunda jogada é:
. Logo, a probabilidade de obtermos, simultaneamente, 2 na primeira
jogada e 5 na segunda jogada é:
Exemplo 6 (UFF - RJ): Em um jogo de bingo são sorteadas, sem reposição, bolas
numeradas de 1 a 75 e um participante concorre com a cartela reproduzida a
seguir. Qual é a probabilidade de que os três primeiros números sorteados
estejam nessa cartela?
Figura 2.3 -
Exemplo de uma cartela de Bingo
Fonte: Elaborada pelos autores.
Solução: Observe
que se trata de eventos independentes. Assim, P (E) =
Exemplo 7: De dois baralhos de 52 cartas retiram-se, simultaneamente, uma carta do
primeiro baralho e uma carta do segundo. Qual a probabilidade da carta do
primeiro baralho ser um rei e a do segundo ser o 5 de paus?
Solução: Como esses
dois acontecimentos são independentes e simultâneos, temos que a probabilidade
de obtermos um rei do primeiro baralho é 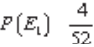 e a probabilidade de se obter o 5 de
paus no segundo baralho é igual a
e a probabilidade de se obter o 5 de
paus no segundo baralho é igual a 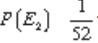 . Logo, a probabilidade de obtermos um rei do
primeiro baralho e um 5 de paus do segundo baralho é:
. Logo, a probabilidade de obtermos um rei do
primeiro baralho e um 5 de paus do segundo baralho é: 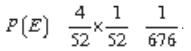
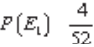 e a probabilidade de se obter o 5 de
paus no segundo baralho é igual a
e a probabilidade de se obter o 5 de
paus no segundo baralho é igual a 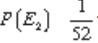 . Logo, a probabilidade de obtermos um rei do
primeiro baralho e um 5 de paus do segundo baralho é:
. Logo, a probabilidade de obtermos um rei do
primeiro baralho e um 5 de paus do segundo baralho é: 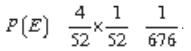
Vejamos, agora,
como proceder ao cálculo da probabilidade para o caso em que os eventos são
mutuamente exclusivos. Dizemos que dois eventos são independentes quando a
realização (ou não realização) de um dos eventos excluiu a realização do outro
e vice-versa. Por exemplo, quando lançamos uma moeda, o evento tirar cara
exclui o evento tirar coroa. No caso de eventos mutuamente exclusivos, a
probabilidade de que um ou outro evento se realize é igual à soma das
probabilidades de realização de cada evento.
Exemplo 8: Em um lançamento de um dado não viciado, qual a probabilidade de se
obter um número não inferior a 5?
Solução: A
probabilidade de se obter um número não inferior a 5 é a probabilidade de se
obter 5 ou 6. A probabilidade de se obter 5 é 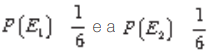 probabilidade de se obter 6.
Assim, a probabilidade de se obter 5 ou 6 é
probabilidade de se obter 6.
Assim, a probabilidade de se obter 5 ou 6 é 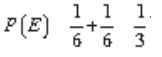
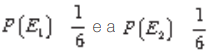 probabilidade de se obter 6.
Assim, a probabilidade de se obter 5 ou 6 é
probabilidade de se obter 6.
Assim, a probabilidade de se obter 5 ou 6 é 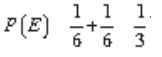
Distribuição de probabilidade
Uma variável
aleatória (normalmente representada por X) é uma variável que assume um único
valor numérico, determinado pelo acaso, para cada resultado de um experimento,
ou seja, é aquela cujos valores são determinados por processos acidentais, ao
acaso, que não estão sob o controle do observador.
Vamos considerar o
caso do lançamento simultâneo de duas moedas não viciadas. Para cada uma
podemos obter CARA ou COROA. Assim, o espaço amostral é S = {(Ca, Ca), (Ca,
Co), (Co, Ca), (Co, Co)}. Digamos que X represente o número de coroas que
aparecem no espaço amostral. Assim, escrevemos a Tabela 1.
Tabela 2.1 - Número
de “coroas” que aparece no espaço amostral do lançamento simultâneo de duas
moedas não viciadas Fonte: Elaborada pelos autores.
Uma distribuição de
probabilidade é uma descrição que dá a probabilidade para cada valor da
variável aleatória. Ela é frequentemente expressa na forma de um gráfico, de
uma tabela ou de uma equação. Assim, podemos reescrever a Tabela 1,
acrescentando a cada valor que aparece COROA a um valor de probabilidade.
Agora, temos a Tabela 2. Assim:
Tabela 2.2 -
Distribuição de probabilidade
Fonte: Elaborada
pelos autores.
Ao definir a distribuição de probabilidade, estabelecemos uma
correspondência unívoca entre os valores da variável aleatória X e os valores
da variável P(X), e essa correspondência define uma função em que os valores
possíveis para a variável aleatória definem o domínio da função e os valores de
P(x) à imagem. Essa função é denominada função probabilidade da variável
aleatória X e é representada por:
Distribuição
binomial A distribuição de probabilidade binomial nos permite lidar com
circunstâncias nas quais os resultados pertencem a duas categorias:
favorável/desfavorável, certo/errado, aceitável/ defeituoso, sucesso/fracasso,
sobreviveu/morreu etc. Dizemos que uma distribuição de probabilidade binomial
resulta de um experimento que satisfaz as seguintes condições:
I.
os experimentos têm
um número fixo de tentativas;
II.
as tentativas devem ser independentes;
III. cada tentativa
deve ter todos os resultados classificados em duas categorias (em
geral,
chamadas de sucesso ou fracasso);
IV. no transcorrer
do experimento, a probabilidade p do sucesso e a probabilidade do insucesso q
manter-se-ão constantes.
Em uma distribuição
de probabilidade binomial, a probabilidade pode ser calculada usando a equação
da probabilidade binomial:
Para x = 0, 1, 2,
3, ..., n. Na equação anterior, n é o número de tentativas; x é o número de
sucessos entre n tentativas; p a probabilidade de sucesso em qualquer
tentativa; q é a probabilidade de fracasso em qualquer tentativa (q = 1 – p).
Exemplo 9: Uma moeda não viciada é lançada 10 vezes seguidas e independentes.
Determine a probabilidade de serem obtidas 6 coroas nessas 10 provas.
Solução: Temos que
n = 10, x = 6, p = 0,5 (pois a probabilidade de COROA ocorrer é ½) e q = 0,5
(pois a probabilidade de CARA ocorrer é ½). Pela lei binomial, escrevemos:
Exemplo 10: Um teste é composto de 7 questões do tipo classificar a sentença como
verdadeira ou falsa. Determine a probabilidade de um candidato que responda
todas ao acaso acertar pelo menos 5.
Solução: Devemos
calcular a probabilidade de se acertar 5, 6 ou 7 questões. A probabilidade de
acertar é p = 0,5 e a probabilidade de errar é 0,5. Temos ainda que n = 7 e x =
5. Assim:
Distribuição normal
Uma variável
aleatória contínua apresenta distribuição com gráfico simétrico e em forma de
sino, como mostra a Figura 4, e que pode ser descrito pela equação:
Figura 2.4 - Distribuição
normal Fonte: Adaptada de Crespo (2009).
I. A variável aleatória X pode assumir todo e
qualquer valor real.
II. A representação gráfica da distribuição
normal é uma curva em forma de sino, simétrica em torno da média, que recebe o
nome de curva normal ou de Gauss.
III. A área total limitada pela curva e pelo eixo
das abscissas é igual a 1, já que essa área corresponde à probabilidade de a
variável aleatória X assumir qualquer valor real.
IV. A curva normal é assintótica em relação ao
eixo das abscissas, isto é, - indefinidamente do eixo das abscissas sem,
contudo, alcançá-lo.
V. Como a curva é simétrica em torno da
média, a probabilidade de ocorrer valor maior que a média é igual à probabilidade
de ocorrer valor menor do que a média, isto é, ambas as probabilidades são
iguais a 0,5 ou 50%. Cada metade da curva representa 50% de probabilidade.
A
distribuição normal padrão é uma distribuição de probabilidade normal média
µ = 0 e desvio-padrão σ=1 e área sob a curva de densidade igual a 1, como
apresentado na Figura 5.
2.5
- Distribuição normal padrão Fonte:
Adaptada de Crespo (2009).
Quando temos em mãos uma variável aleatória
com distribuição normal, nosso principal interesse é obter a probabilidade de
essa variável aleatória assumir um valor em um determinado intervalo. Vejamos
como proceder, por meio de um exemplo.
Exemplo
11:
A concentração de um poluente em água liberada por uma fábrica tem distribuição
normal com média 8 ppm e desvio-padrão 1,25 ppm. Qual a probabilidade de que,
em um dado dia, a concentração do poluente esteja entre 8 e 10 ppm?
Solução: É fácil notar que essa
probabilidade, indicada por P(8 < X < 10), corresponde à área hachurada
na figura a seguir:
Figura
2.6
- Distribuição normal - área entre 8 e 10
Fonte:
Elaborada pelos autores.
Para o cálculo da probabilidade, primeiro
vamos calcular o parâmetro Z. Assim, vamos assumir que Z tem a distribuição
normal reduzida, com média 0 e desvio-padrão 1, ou seja, P(8 < X < 10) =
P(0 < X < 2). Temos que Z é definido como:
Figura
2.7
- Tabela de Distribuição Normal Reduzida
Fonte:
Crespo, 2009, p. 218.
Assim, P(8 < X < 10) = P(0 < X <
2) = 0,4452. Logo, a probabilidade de que, em um dado dia, a concentração do
poluente esteja entre 8 e 10 ppm é de 0,4452 ou 44,52
Exemplo
12:
A concentração de um poluente em água liberada por uma fábrica tem distribuição
normal com média 8 ppm e desvio-padrão 1,25 ppm. Qual a probabilidade de que,
em um dado dia, a concentração do poluente exceda o limite regulatório de 10
ppm?
Solução: É fácil notar que essa
probabilidade, indicada por P(X > 10), corresponde à área hachurada na
figura a seguir:
Figura
2.8
- Distribuição normal - área valores maiores do que 10
Fonte:
Elaborada pelos autores.
Logo, a probabilidade de que, em um dado dia,
a concentração do poluente esteja acima de 10 ppm é de 0,0548 ou 5,48%.
Para o cálculo da probabilidade vamos,
primeiramente, calcular o valor do escore z (ou seja, Z tem a distribuição
normal reduzida, com média 0 e desvio-padrão 1) definido como:
E, em seguida, usar a Tabela de Distribuição Normal
Reduzida do material em anexo. Assim:
Esta unidade foi toda dedicada ao estudo da
probabilidade, que além de ser empregada em jogos de azar, também teve usos
mais remotos por civilizações antigas, como a fenícia, para proteger sua
atividade comercial marítima. Essa teoria começou a ser escrita durante a Idade
Média, para descrever os jogos de azar, e é até hoje muito empregada em outras
ciências, como administração, biologia, medicina e engenharia. A teoria da probabilidade
proporciona um modo de medir a incerteza e de mostrar aos indivíduos como
matematizar, como aplicar a matemática para resolver problemas reais. Começamos
a unidade definindo probabilidade e alguns conceitos básicos. Em seguida,
avançamos para as distribuições de probabilidade: binomial e normal, ambas
muito usadas em situações do nosso dia a dia.
SAIBA
MAIS
A revista SUPERINTERESSANTE publicou, em
agosto de 2012, uma matéria dedicada à sorte. Os autores da reportagem,
Alexandre de Santi e Cristine Kist, afirmam que “Tudo é uma questão de
probabilidade”. Leia essa reportagem, também disponível em: . Acesso em: 15 fev.
2018. E consulte no site da Caixa Econômica Federal (disponível em: . Acesso
em: 15 fev 2018) as probabilidades de você ganhar na Mega Sena.
REFLITA
“A normalidade é tão somente uma questão de
estatística”. Aldous Huxley – Escritor inglês
ATIVIDADES
1) Um consultor está estudando dois
diferentes tipos de imóveis quanto a quantidades disponíveis à venda, por
região, em uma determinada cidade. Os dados são mostrados no quadro a seguir:
Fonte: Elaborado
pelos autores - dados fictícios.
Indique Norte por N; Sul por S; Leste por L;
Oeste por O; Apartamento por A e Casa por C. Determine as seguintes
probabilidades
P(N) =
P(S) =
P(L) =
P(O) =
P(A) =
P(C) =
P(N ∩ A) =
P(S ∩ C) =
P(L ∩ A) =
P(O ∩ C) =
P(N U A) =
P(S U C) =
P(L U A) =
P(O U C) =
2) Em um lote de 15 peças, sendo 5
defeituosas, retira-se uma peça e inspeciona-se. Qual a probabilidade:
a. Da
peça ser defeituosa.
5/15 =
0,333
b. Da
peça não ser defeituosa.
10/15 = 0,666
3) Suponha que a média da taxa de falhas de
dados é transmitida em lotes. Sabe-se que essa característica segue uma
distribuição normal com média de 2 e desvio padrão igual a 0,5. Calcule as
seguintes probabilidades:
a. De tomarmos um lote ao acaso e este ter
uma taxa de falhas entre 2,0 e 2,5.
b. Da taxa de falhas ser maior que 2,1.
c. Da taxa de falhas ser menor que 2,2.
4) Em homens, a quantidade de hemoglobina por
100 ml de sangue é uma variável aleatória com distribuição normal de média
µ=16g e desvio padrão �=1g. Sendo assim, qual a
probabilidade de um homem apresentar mais de 18g de hemoglobina por 100 ml de
sangue?
5) A probabilidade de um atirador acertar o
alvo em um único disparo é de 0,3. Determine qual a probabilidade de que, em 4
disparos, o alvo seja atingido 3 vezes?
INDICAÇÃO
DE LEITURA
Nome do livro: Introdução à Estatística –
Aplicações em Ciências Exatas
Editora: LTC
Autor: Viviane Leite Dias de Mattos; Andréa
Cristina Konrath; Ana Maria Volkmer de Azambuja
Ano: 2017 – 1.ed.
ISBN: 978-85-216-3309-9
Este livro foi elaborado com o intuito de
apresentar alguns conceitos básicos sobre o tema, de maneira simples e
amigável, mas sem se afastar do rigor matemático. Apresenta-nos técnicas de
estatística descritiva, faz uma análise exploratória, aborda tópicos de
probabilidades e distribuição de probabilidades, com exemplos e cases do
cotidiano. O último capítulo apresenta um software livre de estatística e refaz
alguns dos exercícios estudados ao longo dos capítulos anteriores.
ANEXO
Tabela
de distribuição Normal Reduzida
Tabela
2.1: Tabela de distribuição Normal Reduzida Fonte: Crespo, 2009, p. 218.
Correlação
e Regressão
INTRODUÇÃO
Nesta unidade introduziremos um método para a
determinação da existência ou não de uma correlação, ou associação, entre duas
variáveis para o caso dessa correlação ser linear. Quando se trabalha com duas
ou mais variáveis, elas poderão estar ou não relacionadas. Se essas variáveis
estiverem relacionadas, iremos estabelecer uma equação matemática que
estabeleça o grau dessa dependência. Para tal, identificaremos uma função
polinomial do primeiro grau que melhor se ajusta aos dados e a partir disso
poderemos empregar esta equação para predizer o valor de uma variável, dado o
valor da outra.
CORRELAÇÃO
E REGRESSÃO LINEAR
Dizemos que duas variáveis estão ligadas por
uma relação estatística quando existe correlação entre elas, ou seja, existe
correlação entre duas variáveis quando os valores de uma variável estão
relacionados, de alguma maneira, com os valores de outra variável.
Vejamos alguns exemplos: a idade e altura das
crianças; o tempo de prática de esportes e ritmo cardíaco; o tempo de estudo e
a nota na prova; a taxa de desemprego e a taxa de criminalidade; a expectativa
de vida e a taxa de analfabetismo; a taxa de juro e a inflação.
As variáveis altura e peso de uma criança
recém-nascida, por exemplo, apresentam-se, em geral, correlacionadas
positivamente, pois assim que a criança “ganha altura”, ela também “ganha
peso”. Por outro lado, no Brasil, as variáveis renda familiar e o número de
elementos da família costumam se apresentar correlacionados negativamente, pois
as famílias de baixa renda, em geral, tendem a ter mais filhos do que as de
alta renda. Quando se trabalha com duas variáveis, diz-se correlação e
regressão simples.
Quando se trabalha com mais de duas
variáveis, fala-se de correlação e regressão múltipla.
A
Figura 1 ilustra algumas correlações. Vejamos:
Figura
1 - Tipos de correlação Fonte:
Adaptada
de Crespo (2009)
Uma correlação linear simples é uma relação
entre duas variáveis quantitativas, tais que os dados são representados por
pares ordenados, (X, Y), em que X é a variável independente (explicativa) e Y é
a variável dependente (resposta).
Antes de realizar qualquer análise
estatística formal sobre regressão, devemos usar um diagrama de dispersão para
explorar os dados coletados visualmente. Coletam-se dados exibindo os valores
correspondentes das variáveis. Assim, faz-se o gráfico com os dados coletados
em um sistema de coordenadas retangulares. O conjunto resultante é chamado
diagrama de dispersão, que é uma maneira de visualizarmos se duas variáveis
apresentam-se correlacionadas. Veja a Figura 1.
Para ficar claro, vejamos a seguinte situação
problema: o administrador da rede de Lojas Canção está interessado em descobrir
se existe relação entre os gastos com propaganda das lojas, no horário nobre da
TV aberta, e as vendas dessas lojas. Para tal propósito, ele conduz um estudo
para determinar se existe uma relação linear entre o dinheiro gasto em
propaganda e as vendas. Os dados coletados pelo administrador estão dispostos
na tabela a seguir.
Tabela 1 - Gastos com propagandas e vendas da
loja
Fonte:
Elaborada pelos autores.
Representando, em um sistema de coordenadas
cartesianas ortogonais, os pares ordenados (Xi , Yi ), obtemos o diagrama de
dispersão, o qual nos mostra a existência de correlação entre as variáveis
estudadas.
Figura
2
- Diagrama de dispersão
Fonte:
Elaborada pelos autores.
Desprende-se da Figura 2 que existe
correlação positiva entre as variáveis “gastos” com propaganda e “vendas”, ou
seja, o aumento com gastos com propagandas ocasiona aumento nas vendas das
lojas.
Podemos determinar a intensidade com que
esses dados estão correlacionados, calculando o coefi ciente de correlação de
Pearson que é dado por:
Em que n é o número de observações. Os
valores de r estão no intervalo. Assim:
I.
Se a correlação entre as variáveis é perfeita
e positiva, então r = 1.
II.
Se a correlação entre as variáveis é perfeita
e negativa, então r = - 1.
III.
Se não existe correlação entre as variáveis,
então r = 0. Nesse caso, obviamente, a correlação não é linear.
IV.
Se a correlação é de inexistente a muito
fraca e nada podemos concluir.
V.
Se a correlação é muito fraca à média e
podemos considerar o valor de r nesse intervalo como indício de uma correlação
entre as variáveis sem muito efeito.
VI.
Se a correlação é de média a muito forte e as
variáveis mantêm dependência significativa.
Vamos calcular r para o caso do Quadro 1.
Vejamos a seguir:
Quadro
1 - Cálculo da correlação linear
Fonte:
Elaborado pelos autores
Com o valor de r calculado, pode-se afirmar
que, de fato, há forte correlação positiva entre as variáveis “gastos”e vendas.
Agora, é interesse determinar uma equação em que a e b são números
reais. Assim, supondo X que é a variável independente e Y que é a variável
dependente, vamos determinar o ajustamento de uma equação de reta, que é a
relação entre esses dados. Os valores de a
e de b são dados por:
Assim, temos a reta de regressão para o exemplo estudado como: Y = 0,013x - 1,25.
Para traçar a reta no plano formado pelos eixos X e Y, basta atribuir, pelo
menos, dois valores para X e calcular os correspondentes valores de Y, pois,
por dois pontos passa uma, e apenas uma reta.
REFLITA
Observe
como a regressão linear está presente em análises que fazemos no nosso
cotidiano. Fonte: Os autores.
Mas, qual o significado dessa equação? Com
relação às oito filiais estudadas, podemos predizer as vendas de uma filial (Y)
a partir de um dado gasto com propaganda (X), fazendo uso da equação . Por
exemplo, para um gasto com propaganda de X = R$ 2000, temos uma estimativa para
as vendas de (em R$ 1000). Observe que quando não se gasta com propaganda
(X=0), prevemos uma queda nas vendas de US$1,25 (US$1000).
Vimos que, se verificarmos a existência da
correlação entre duas variáveis, X e Y, podemos determinar uma equação linear,
que expressa Y em função de X e que essa equação nos permite o cálculo de Y,
conhecido o X. Temos que ter em mente que um valor previsto para Y não será
necessariamente um resultado exato, pois além do valor da variável X, existem
outras variáveis que não foram incluídas no estudo e essas podem afetar o
resultado final. O coeficiente de
determinação (r2 ) é o quadrado do coeficiente de correlação, ou
seja, [Coeficiente de determinação =
(coeficiente de correlação)2 ] é uma medida descritiva da
proporção da variação de Y que pode ser explicada por X, segundo o modelo
especificado. No exemplo em que estudamos a relação linear dinheiro gasto em
propaganda e as vendas das lojas Canção, obtemos um coeficiente de correlação
de r = 0,9899. Então, r2 = 0,9799 ou 97,99% e a interpretação desse coeficiente
de determinação é que dentre as filiais estudadas, 97,99% da variação nas
vendas dessas filiais são explicadas pela variação nos gastos com propaganda.
Os 2,01% (1 - 0,9799 ou 100-97,99) restantes são inexplicáveis e se devem ao
acaso ou a outras variáveis.
Começamos nossos estudos com uma variável de
interesse e estudamos na Unidade I as medidas de tendência central, de
dispersão, de assimetria e curtose. Nessa unidade, com duas ou mais variáveis,
além destas medidas individuais, também é de interesse conhecer se elas têm
algum relacionamento entre si, e se valores altos (baixos) de uma das variáveis
implicam em valores altos (ou baixos) da outra variável. Na Unidade III
estudamos o relacionamento entre duas variáveis por meio de regressão linear
simples. Vimos que a regressão e a correlação tratam apenas do relacionamento
do tipo linear entre duas variáveis e que a análise de correlação entre essas
variáveis fornece-nos um número que resume o grau de relacionamento linear entre
as duas variáveis em estudo. Já a análise de regressão fornece uma equação a
qual descreve o comportamento de uma das variáveis em função do comportamento
da outra variável.
SAIBA
MAIS
Existem diversos estudos tentando encontrar
ao menos uma correlação entre algumas variáveis. Pessoas inteligentes comem
muito chocolate Comem chocolate, ficam inteligentes e ganham prêmios. Parece
bobagem, mas existe uma relação entre o consumo de chocolate e os países onde
vivem os vencedores do Prêmio Nobel. E quem fez essa comparação realmente não
tinha mais nada para fazer. O cardiologista Franz Messerli estava deitado em um
quarto de hotel quando parou para pensar sobre um estudo que mostrava como o
flavonoide do cacau pode aprimorar nossas habilidades cognitivas. Aí ele
começou a analisar se os países de onde mais saíam vencedores do Prêmio Nobel
consumiam muito chocolate. E concluiu: quanto maior o consumo de chocolate per capita (kg/habitantes) de um país, maior o número de gênios
premiados com o Nobel, a cada 10 milhões de pessoas.
Os suíços, por exemplo, que somam quase 8
milhões de pessoas, já levaram 29 premiações e comem chocolate para caramba –
cada habitante come quase 10 quilos do doce por ano. A Suécia e Alemanha
também. Seguindo a média encontrada pela pesquisa, para ganhar mais um Nobel,
qualquer país precisa aumentar em 400 gramas o consumo anual de chocolate.
Bobeira? Total. Até o pesquisador sabe: ninguém vai ganhar um Nobel depois de
se entupir de chocolate. Mas se esse pessoal inteligente curtia uma barra de
chocolate, por que não seguir o exemplo? Fonte: CASTRO, C. Pessoas inteligentes
comem muito chocolate. Super
Interessante. 21 dez. 2016. Disponível em: . Acesso em: 14 fev. 2018.
SAIBA
MAIS
“Ganhar um Oscar aumenta a expectativa de
vida!” É o que afirma Hanet et al. da Universidade de
Princeton. O artigo está disponível em: . Acesso em: 18 fev. 2018. Neste nosso
estudo vimos a importância da correlação e regressão linear.
Estudamos a força da relação de duas
variáveis (x e y) por meio da correlação linear.
Vimos que, para estudar a correlação linear,
seu principal objetivo é avaliar a existência ou não de relação entres essas
variáveis, quantificando a força dessa relação por meio da correlação, ou
explicando a forma dessa relação por meio da regressão. As correlações podem
ser Positivas, quando o aumento de uma variável corresponde ao aumento da
outra; Negativas, quando o aumento de uma variável corresponde à diminuição da
outra; Lineares, quando é possível ajustar uma reta, que podem ser fortes (quanto
mais próximas da reta) ou fracas (quanto menos próximas da reta), e ainda Não
Lineares, quando não é possível ajustar uma reta. Após estabelecida uma relação
linear e uma boa correlação entre as variáveis, deve-se, agora, determinar uma
fórmula matemática para se fazer predições de uma das variáveis por meio da
outra, e a essa técnica damos o nome de Análise de Regressão.
INDICAÇÃO
DE LEITURA
Nome do livro: Estatística Aplicada
Editora: Pearson
Autor: Ron
Larson, Betsy Farber
ISBN: 9788543004778
Esse livro traz itens essenciais à
estatística tais como probabilidades, correlação e regressão linear e teste de
hipóteses, além de contar com resolução de exercícios.
INDICAÇÃO
DE LEITURA
Nome do livro: Estatística Teoria e
Aplicações
Editora: LTC
Autor: David M. Levine, David F. Stephan,
Kathryn A. Szabat
Ano: 2016 – 7 ed.
ISBN: 978-85-216-3067-8
Este livro apresenta a utilização da teoria
estatística com aplicação do Microsoft Excel. É uma obra essencial para aqueles
que buscam a pesquisa e a análise, pois mostra ferramentas, conceitos e dados
práticos em sua abordagem. Traz inúmeros exercícios, resolvidos por formas
algébricas e pelo Excel.
CONTINUAÇÃO-> MÉTODOS QUANTITATIVOS ESTATÍSTICOS 3














































