- Não há como transformar uma superfície esférica em um mapa plano sem que ocorram distorções.
- Cada projeção é adequada a um tipo de aplicação
-Na impossibilidade de se desenvolver uma superfície esférica ou elipsóidica sobre um plano sem deformações, na
prática, buscam-se projeções tais que permitam diminuir ou eliminar parte das deformações conforme a aplicação desejada. Assim, destacam-se:
a) Eqüidistantes - As que não apresentam deformações lineares para algumas linhas em especial, isto é, os comprimentos são representados em escala uniforme.
b) Conformes - Representam sem deformação, todos os ângulos em torno de quaisquer pontos, e em
decorrência dessa propriedade, não deformam pequenas regiões.
c) Equivalentes - Têm a propriedade de não alterar as áreas, conservando assim, uma relação constante com as suas correspondentes na superfície da Terra. Seja qual for a porção representada num mapa, ela conserva a mesma relação com a área de todo o mapa.
d) Afiláticas - Não possui nenhuma das propriedades dos outros tipos, isto é, equivalência, conformidade e eqüidistância, ou seja, as projeções em que as áreas, os ângulos e os comprimentos não são conservados.
-Uma projeção é uma transformação matemática. Há projeções sem um análogo geométrico simples.
a) Planas
b) Cônicas
c) Cilíndricas
d) Polissuperficiais - se caracterizam pelo
emprego de mais do que uma superfície de
projeção (do mesmo tipo) para aumentar o
contato com a superfície de referência e, portanto, diminuir as deformações (planopoliédrica; cone-policônica ; cilindropolicilíndrica).
PROJEÇÕES MAIS USUAIS E SUAS CARACTERÍSTICAS
PROJEÇÃO POLICÔNICA
- Superfície de representação: diversos cones
- Não é conforme nem equivalente (só tem essas características próxima ao Meridiano Central).
- O Meridiano Central e o Equador são as únicas retas da projeção. O MC é dividido em partes iguais pelos paralelos e não apresenta deformações.
- Os paralelos são círculos não concêntricos (cada cone tem seu próprio ápice) e não apresentam deformações.
- Os meridianos são curvas que cortam os paralelos em partes iguais.
- Pequena deformação próxima ao centro do sistema, mas aumenta rapidamente para a periferia.
- Aplicações: Apropriada para uso em países ou regiões de extensão predominantemente Leste-Oeste e reduzida extensão Norte-Sul.
No BRASIL é utilizada em mapas da série Brasil, regionais, estaduais e temáticos.
PROJEÇÃO CÔNICA NORMAL DE LAMBERT (com dois paralelos padrão)
- Cônica.
- Conforme.
- Analítica.
- Secante.
- Os meridianos são linhas retas convergentes.
- Os paralelos são círculos concêntricos com centro no ponto de interseção dos meridianos.
- Aplicações: A existência de duas linhas de contato com a superfície (dois paralelos padrão) nos fornece uma área maior com um baixo nível de deformação. Isto faz com que esta projeção seja bastante útil para regiões que se estendam na direção este-oeste, porém pode ser utilizada em quaisquer latitudes.
A partir de 1962, foi adotada para a Carta Internacional do Mundo, ao Milionésimo.
PROJEÇÃO CILÍNDRICA DE MERCATOR (Tangente)
- Cilíndrica.
- Conforme.
- Analítica.
- Tangente (ao Equador).
- Aplicações: Indicada para representações de todo o planeta.
- Problema, grande distorção de áreas em regiões distantes do Equador.
PROJEÇÃO CILÍNDRICA TRANSVERSA DE MERCATOR (Tangente)
- Cilíndrica.- Conforme.
- Analítica.
- Tangente (a um meridiano).
- Os meridianos e paralelos não são linhas retas, com exceção do meridiano de tangência e do Equador.
- Aplicações: Indicada para regiões onde há predominância na extensão Norte-Sul. É muito utilizada em cartas destinadas à navegação.
- Cilíndrica.
- Conforme.
- Secante.
- Só o Meridiano Central e o Equador são linhas retas.
- Projeção utilizada no SISTEMA UTM - Universal Transversa de Mercator desenvolvido durante a 2ª Guerra Mundial. Este sistema é, em essência, uma modificação da Projeção Cilíndrica Transversa de Mercator.
- Aplicações: Utilizado na produção das cartas topográficas do Sistema Cartográfico Nacional produzidas pelo IBGE e DSG.
* a. Um cilindro que toca o globo em um meridiano central de uma zona de longitude está completamente fora do globo e regiões distantes do meridiano central são representadas com área maior que a real.
* b. Um cilindro que toca o globo nas bordas de uma zona de longitude (secante) está dentro do globo naquela zona, regiões dentro da zona terão projeções com área menor que a real.
* c. Assim escolheu-se um ponto ótimo para passar a secante, de forma que as distâncias de toda a zona são semelhantes às reais. Essa posição está a 180 km do meridiano central da zona.
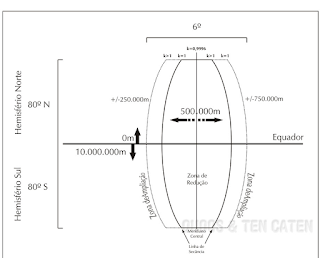
Sistema universal de Projeção Transversa de Mercator (UTM)
- 60 cilindros tangenciais a meridianos a 6o de distância cobrem toda a superfície terrestre, gerando 60 fusos UTM.
- Como a distância máxima entre o meridiano central de cada fuso e as bordas desse fuso é de apenas 3o, a distorção é pequena.

-As linhas norte-sul da projeção são paralelas à direção norte real apenas no meridiano central de cada fuso, podendo divergir até 3o nas bordas (em altas latitudes).
-O sistema permite a atribuição de coordenadas em metros a partir de uma origem imaginária a 500 km a oeste do meridiano central de cada cilindro e no extremo sul do hemisfério (no hemisfério sul a origem é o Pólo e no norte é o Equador).
-O sistema UTM define zonas, baseadas na subdivisão de cada fuso de 6o de longitude em áreas de 8o de latitude (5o acima das latitude 80o N e S).
-A denominação de cada zona é feita da seguinte forma:
O número do fuso, contando a partir do meridiano 180o, para leste e uma letra de A a Z a partir do Pólo Sul (exclui-se I e O por parecerem números).
Como a divisão da carta topográfica internacional ao milionésimo é de 6o de longitude por 4o de latitude, e parte também do meridiano 180o para leste, cada zona UTM coincide com duas folhas
topográficas 1:1000000.
Problemas do Sistema UTM
- É inadequado para escalas pequenas, pois aparecem distorções.
- Cada fuso UTM é uma projeção diferente, não se pode unir mapas de dois fusos nesse sistema de projeção. - Deve-se notar que as linhas N-S da projeção não são paralelas à direção N-S verdadeira (com exceção do meridiano central).
- Como as coordenadas são em metros e a malha é aparentemente constante, o usuário sem informação pode pensar que o sistema é um gráfico cartesiano, sem perceber as limitações da projeção.
Não se pode unir mapas de dois fusos. Uma pequena sobreposição (40 km) entre os fusos evita a necessidade de modificação do sistema de projeção para áreas pequenas nos limites entre fusos. Para áreas grandes (escalas pequenas) nessa situação, é necessário utilizar outra projeção.
Porção da Europa Ocidental mostrando a sobreposição de um mapa composto de vários fusos UTM (em amarelo) e um mapa com projeção ortográfica com mesmo centro (em azul). Notar a grande distorção.
Mesmo mapa mostrando a sobreposição de uma projeção cônica de Lambert (contorno preto) e uma projeção ortográfica com mesmo centro (em azul). As duas projeções são muito semelhantes e de pequena distorção nessa escala.
- No Equador não há obliquidade entre as linhas N-S da projeçao UTM e a direção N-S real.
- Com o aumento da latitude e o afastamento do meridiano central, a obliquidade aumenta, chegando a três graus na borda do fuso a 90o de latitude.
- Na latitude de São Paulo a borda do fuso está a ~306Km
(3o), e a obliquidade nessa faixa é de ~1,2o.
- Na mesma latitude, a 102 km do meridiano central (1o), a obliquidade é de ~0,4o.
- Na latitude de Porto Alegre a borda do fuso está a ~289 km do meridiano central, e a obliquidade nessa faixa é de ~1,5o.
- Na mesma latitude, a 96 km do meridiano central (1o), a
obliquidade é de ~0,5o.
- Mesmo sendo elaborados com projeção UTM, os mapas de escala 1:50.000 e 1:10.000 também são limitados por meridianos e paralelos, e pode-se notar a obliquidade das linhas de UTM com os limites dos mapas.
Conclusões
- A projeção UTM é útil em áreas pequenas, em escalas 1:50.000 ou 1:10.000.
- O sistema UTM não dá coordenadas cartesianas em metros, pois sua malha é distorcida em relação às direções N-S e E-O verdadeiras.
- Não se pode integrar mapas de fusos diferentes, ou seja, se dois mapas 1:10.000 adjacentes apresentam sigla inicial com número diferente (SF22 e SF23, por exemplo), isso indica que estão em cartas 1:1.000.000 diferentes, e portanto em fusos UTM diferentes, cada um projetado em um cilindro.
- Na latitude de São Paulo os limites de um fuso tem inclinação de 1,2o em relação ao norte geográfico, e como mapas de fusos adjacentes tem inclinação oposta, as linhas UTM divergem em 2,4o – os mapas não encaixam.
- Para indicar a posição de um ponto no planeta, não basta fornecer as coordenadas lidas em um GPS, é necessário informar também a zona UTM, pois uma determinada coordenada pode representar 120 pontos diferentes no planeta, 2 por cilindro (um Norte e outro Sul).
- Em projetos e relatórios de áreas restritas é útil expressar a posição de um ponto em UTM, mas para
trabalhos regionais ou destinados a publicação em periódicos, as coordenadas geográficas são mais
adequadas.



















