ATIVIDADES
1)
(UEL-PR) Considerando os coeficientes de correlação, relacione a coluna da
esquerda com os respectivos diagramas de dispersão, na coluna da direita.
Assinale a alternativa que contém a
associação correta.
a. I-A, II-B, III-E, IV-D, V-C.
b. I-A, II-E, III-C, IV-B, V-D.
c. I-B, II-A, III-D, IV-E, V-C.
d. I-B, II-A, III-E, IV-D, V-C.
e. I-C, II-A, III-D, IV-B, V-E.
2) Um pesquisador resolveu fazer uma pesquisa
em um curso superior, relacionando as disciplinas de Matemática e Química. Para
realizar esse estudo, durante 20 dias foram coletadas as notas de 40 acadêmicos
em ambas as disciplinas. Com base nessas amostras, foi solicitado a um
estatístico que fizesse algumas observações sobre a existência de alguma
relação entre as disciplinas de Matemática e Química. Esse estatístico avaliou
os resultados da pesquisa, calculou o coeficiente de correlação de Pearson e
obteve um valor de 0,87. Com base neste resultado, podemos afirmar que:
a. Existe uma forte relação entre as
disciplinas de Matemática e Química, uma vez que o coeficiente de correlação de
Pearson apresentou um valor muito próximo de 1.
b. Não
existe uma forte relação entre as disciplinas de Matemática e Química, uma vez
que o coeficiente de correlação de Pearson apresentou um valor muito próximo de
1.
c. Existe uma fraca relação entre as
disciplinas de Matemática e Química, uma vez que o coeficiente de correlação de
Pearson apresentou um valor muito próximo de 1.
d. Não existe uma relação entre as
disciplinas de Matemática e Química, uma vez que o coeficiente de correlação de
Pearson deveria apresentar valores próximos de zero para essa afirmação.
e.
Para que exista uma forte correlação entre as disciplinas de Matemática e
Química, o coeficiente de Pearson deveria ser entre 0,3 a 0,6.
3) A correlação entre as disciplinas de
Português (x) e Inglês (y) é de 0,89. A equação de regressão linear é de y =
0,412x + 4,895. Se a nota de um aluno na disciplina de Português é 7,0; qual
será sua nota em Inglês?
a. 7,0.
b. 7,5.
c. 7,8.
d. 8,0.
e. 9,2
4) Em Estatística, o termo correlação é usado
para indicar a força que mantém unidos dois conjuntos de valores. O estudo da
correlação tem como objetivo estudar a existência ou não de uma relação e seu
grau de relação entre as variáveis. As notas de 8 alunos do curso de
Administração estão apresentados na Tabela a seguir:
Dados para resolução: Correlação das notas de
Contabilidade de Custos e Estatística:
0,95.
Mediante do exposto, leia as afirmativas a
seguir.
I.
Podemos afirmar que existe uma correlação
fraca entre as disciplinas de Matemática Financeira e Estatística.
II.
Podemos afirmar que existe uma correlação
forte entre as disciplinas de Matemática Financeira e Estatística.
III.
Se fizermos um gráfico de dispersão para
representar a correlação entre as disciplinas de Matemática Financeira e
Estatística, ele será crescente.
IV.
Se fizermos um gráfico de dispersão para
representar a correlação entre as disciplinas de Matemática Financeira e
Estatística, ele será decrescente.
É correto o que se afirma em:
a. I e II, apenas.
b. II e III, apenas.
c. I e III, apenas.
d. I, II e III, apenas.
e. I, II e IV, apenas.
5) Existem algumas medidas estatísticas que
permitem medir o grau de associação entre duas variáveis: a correlação linear e
a regressão linear. Sobre a correlação e regressão linear, leia as afirmativas
a seguir:
I. A
correlação é utilizada para indicar a força que mantém unidos dois conjuntos de
valores.
II. O
estudo da correlação tem por objetivo estudar a existência ou não e seu grau de
relação entre as variáveis.
III. Quanto ao direcionamento entre as duas
variáveis, o coeficiente de correlação pode ser positivo ou negativo. Se a
correlação entre duas variáveis for positiva, dizemos que as duas variáveis x e
y variam para o mesmo sentido.
IV. A análise de regressão é uma técnica
estatística cujo objetivo é investigar e descrever a relação entre variáveis
mediante um modelo matemático.
Diante disso, é correto o que se afirma em:
a. I e II, apenas.
b. I e III, apenas.
c. II e III, apenas.
d. I, II e III, apenas.
e. I, II, III e IV.
A apostila "Fórmulas da Apostila de
Estatística" (em PDF) é um material complementar da disciplina Métodos
Quantitativo Estatísticos, o qual contém as fórmulas e as respectivas páginas
da apostila, nas quais o conteúdo (fórmula) está inserido.
Prova 1
1 - Observe a nota que um aluno atingiu nos
quatro bimestres em Matemática:
Nessa escola, a média necessária para
concluir a disciplina é 7,5. Nesse caso, podemos afirmar que:
Escolha uma:
2 - Rômulo pesquisou a idade dos jogadores da
seleção brasileira de futebol:
Rômulo deseja fazer uma tabela de
distribuição de frequências, a qual apresentará, usando a fórmula de Sturges:
Escolha uma:
3 - A tabela de distribuição de frequências
dos dados abaixo exibirá intervalos com amplitude igual a:
Escolha uma:
4 - Analise o seguinte conjunto de valores e
determine a moda desse conjunto:
Escolha uma:
5 - É possível obter a frequência relativa
acumulada:
Escolha uma:
6 - Constitui-se uma amostragem sistemática
de 8 elementos, para uma população de 400. Se o primeiro elemento sorteado para
a amostra foi o 24, o terceiro será o:
Escolha uma:
Constitui-se uma amostragem (...)
400 / 8 = 50 (para ter uma amostragem estratificada, irá contar de 50 em 50).
Se o primeiro foi 24, o segundo será 74 (24 + 50) e o terceiro será 124 (74 + 50).
400 / 8 = 50 (para ter uma amostragem estratificada, irá contar de 50 em 50).
Se o primeiro foi 24, o segundo será 74 (24 + 50) e o terceiro será 124 (74 + 50).
7 - A idade dos jogadores da seleção
brasileira de futebol está presente na tabela abaixo:
Podemos afirmar que a idade média aproximada
desses jogadores é de:
Escolha uma:
8 - Após uma festa de aniversário, o dono do
buffet deseja saber o grau de satisfação dos convidados. Para isso, ele precisa
de uma amostra aleatória estratificada de 20% de todos os presentes. Sabe-se
que participaram da festa 120 crianças, 80 mulheres e 50 homens.
Desta forma, o dono do buffet deve questionar:
Escolha uma:
Após uma festa de aniversário...
Crianças = 120 x 20% = 24 crianças
Mulheres = 80 x 20% = 16 mulheres
Homens = 50 x 20% = 10 homens
Crianças = 120 x 20% = 24 crianças
Mulheres = 80 x 20% = 16 mulheres
Homens = 50 x 20% = 10 homens
9 - A tabela a seguir mostra as
notas dadas de 0 à 5 para o atendimento de telemarketing de uma empresa:
Considerando que, para avaliar seus
funcionários, a empresa levará em conta a medida de posição MODA, então a nota
será:
Escolha uma:
10 - A professora de Educação Física tabelou
a estatura dos alunos de uma das suas turmas:
A melhor estimativa de altura para o terceiro
decil da distribuição de frequência dos alunos é:
Escolha uma:
A professora de Educação Física (...)
O primeiro passo é identificar onde está o terceiro decil (30%) dos dados.
Sabendo que tem 40 alunos, o terceiro decil será 12 alunos. Assim, está na classe 155 |---- - 160, a qual se estende até o 13.
Agora, basta aplicar a fórmula da interpolação linear:
onde: y = 12 (30 % de 40).
X = variável.
X1 = 155
X2 = 160
Y1=13
Y2 = 4
12 = 4+ ⌊((X-155))/((160-155)) X (13-4)⌋
12 = 4 + ⌊((X-155))/5 X 9⌋
12 = 4 + [(9X-1395)/5]
8 = [(9X-1395)/5]
9X – 1395 = 40
9X = 40 + 1395
9 X = 1.435
X = 1435 / 9
X = 159,44 cm ou seja 1,59 m.
1 - Um veterinário realizou uma pesquisa para
saber a média das idades dos 50 animais presentes na clínica (entre felinos e
caninos) e registrou na seguinte tabela:
A idade média dos seus pacientes é:
Escolha uma:
Um veterinário (...)
O número de elementos é 50, e a soma total das idades é 286 (12 + 24 + 75 + 100 + 75), desta forma a média aritmética das notas é 5,72 (286/50).
12x1+3x8+5x15+10x10+15x5/12+8+15+10+5= 286/50=5,72
2 - Analise os dados dispostos na tabela
abaixo:
A moda e a mediana dos valores desta tabela
são, respectivamente:
Escolha uma:
3 - Um professor de matemática fez a média
aritmética das seguintes notas obtidas pelos seus alunos na prova:
A média das notas é:
Escolha uma:
4 - Para poder solicitar uma prova
substitutiva, um professor impôs o seguinte critério para o aluno: a nota dele
deverá estar abaixo da nota mediana da turma. Considerando a tabela de notas da
turma abaixo, podemos afirmar que o número de alunos que poderá fazer a
solicitação desta prova é:
Escolha uma:
5 - O ponto médio da classe de maior
frequência absoluta do histograma abaixo é:
Escolha uma:
O ponto médio da classe (...)
A classe de maior frequência possui 50, que é 2,0 a 2,5.
Para calcular o ponto médio, basta somar o limite inferior da classe ao limite superior da classe e dividir por 2.
Desta forma, ficaria: 2,0 + 2,5 = 4,5 / 2 = 2,25.
6 - Considere a seguinte tabela:
Deseja-se escolher aleatoriamente 4 frutas
para consumo durante um mês (uma fruta por semana). Utilizando a tabela
de números aleatórios abaixo (da esquerda para a direita, de dois em
dois dígitos):
Podemos dizer que as frutas escolhidas serão:
Escolha uma:
Explicação: A tabela de frutas estão
numeradas até o numero 25, então dentre os números aleatórios que o exercício
oferece temos que escolher quatro frutas dentro desse quadro de números, ou
seja temos que escolher números do 01 ao 25 que são : 18 , 25 , 03, 07
que são referente as numerações das frutas.
92 59 18 52 87 35 25 93 88 74
03 62 98 38 58 65 86 42 41 07
7 - Com relação às medidas de tendência
central presentes na tabela abaixo, podemos afirmar que:
Escolha uma:
Com relação às medidas de tendência (...)
O número total de elementos é 50 (total das frequências absolutas).
Sendo assim, a mediana será: 51/2 = 25,5 (está no número 5 = somando 12 + 8 + 15, resulta em 35, portanto, o 25,5 está na classe do 5).
A moda, é o valor que possui a maior frequência absoluta, neste caso, seria o 5 (foi citado 15 vezes).
Como ambos – mediana e moda, pertencem a classe do número 5.
8 - De acordo com o histograma abaixo,
podemos afirmar que a amplitude total é de:
Escolha uma:
9 -Podemos afirmar que o conjunto de dados
abaixo é:
Escolha uma:
10 - Um supermercado fez uma promoção
diferente. Cada cliente que comprasse neste dia teria direito a escolher um
algarismo de 0 à 9. Ao final, um prêmio de R$ 200,00 em consumação seria
sorteado entre os clientes que escolheram um algarismo que pertencesse à classe
mediana das escolhas:
Participarão do sorteio os clientes que
escolheram os números:
Escolha uma:
Um supermercado fez uma promoção (...)
O primeiro passo é calcular n / 2. Considerando que n = 100, então n/2 = 50.
50 está na classe 2ª classe: 2 |------ 4.
Assim, quem escolheu 4, está fora do sorteio. Ou seja, os clientes que escolheram 2 ou 3 participarão do sorteio.
1 - Um jogo de bingo contém números de 1 à
75. Já saíram os números 22, 53, 56, 19, 8, 73, 20, 36, 43 e 71. Neste
instante, Karen e Heloísa gritaram “BINGO” juntas, pois ambas completaram os
quatro cantos da cartela. Para ganhar o prêmio, precisavam tirar a pedra maior.
Sabendo que Karen retirou o número 38, qual a probabilidade de Heloísa ganhar o
prêmio?
Escolha uma:
a.
25%.
b.
50%. X
c.
60%.
d.
75%.
e.
80%.
Um jogo de Bingo (...)
Antes de aplicar a fórmula, perceba que 38 é a mediana dos dados.
Ou seja, de 1 a 37 (metade) – 38 (mediana) - 39 a 75 (metade)
Haviam sido retiradas 10 bolas: 5 bolas antes da mediana – (8, 19, 20, 22 e 36) e 5 bolas depois da mediana – (43, 53, 56, 71 e 73).
Total de bolas (75) – bolas retiradas (11) = 64 bolas para serem sorteadas.
Considerando que a Karen retirou exatamente a mediana, assim, Heloisa pode tirar ou 1 bola maior ou 1 bola menor, já que o número de bolas maiores ou menores no globo, é igual.
P (E) = (n (E))/(n (S))
P (E) = (1 (bola))/(2 (maior ou menor))
P (E) = 0,50 ou 50%
Explicação:
só ver as opções maiores que 38, de 10
números sorteados 5 são maiores, fica 5/10,sendo assim 50%
2 - Sabe-se que um baralho de cartas possui
52 cartas diferentes, com 4 naipes diferentes (ouro, paus, copas e espadilha),
sendo 13 cartas de cada naipe. Qual a probabilidade de Diogo retirar uma carta
do naipe ouro de um baralho com 52 cartas?
Escolha uma:
a.
10%.
b.
15%.
c.
20%.
d.
25%. X
e.
30%.
Sabe-se que um baralho de cartas (...)
Basta aplicar a fórmula:
P (E) = (n (E))/(n (S))
P (E) = (1 (uma carta de ouro))/(4 (quantidade de naipes possíveis))
P (E) = 0,25 ou 25%.
Basta aplicar a fórmula:
P (E) = (n (E))/(n (S))
P (E) = (1 (uma carta de ouro))/(4 (quantidade de naipes possíveis))
P (E) = 0,25 ou 25%.
3 - A diretora de uma escola vai sortear uma
viagem para dois entre os 50 alunos do 9º ano. Qual a probabilidade de Ana e
Luiza, que são muito amigas, irem a essa viagem juntas?
Escolha uma:
a.
1/2500.
b.
2/500.
c.
1/2450. X
d.
2/2450
e.
99/2450
A diretora de uma escola (...)
Na primeira tentativa: 1/50
Na segunda tentativa: 1/49.
Assim, para saber a probabilidade tem que multiplicar: P1 x P2 = 1/50 x 1/49 = 1/2450.
(multiplicação de fração: multiplica numerador por numerador e denominador por denominador).
4 - Sabendo que as notas de um aluno são 4,0
no primeiro bimestre, 6,0 no segundo bimestre, 6,5 no terceiro bimestre e 8,0
no quarto bimestre, calcule os desvios em relação à média.
Escolha uma:
a.
2,125; 0,125; -0,375; -1,875.
b.
-2,125; -0,125; 0,375; 1,875. X
c.
-2,125; 0,125; -0,375; 1,875.
d.
-2,125; -0,125; -0,375; -1,875.
e.
2,125; 0,125; 0,375; 1,875
Sabendo que as notas (...)
O conteúdo está na Unidade, pp. 68-72.
Considerando que o número de notas é 4, e a soma total das notas foi 24,5, a média foi de 6,125.
Agora, basta calcular a diferença entre cada nota e a média (6,125).
1º Bimestre: 4, assim: Nota – Média = 4 – 6,125 = (-2,125)
2º Bimestre: 6,0, assim: Nota – Média = 6,0 – 6,125 = (-0,125)
3º Bimestre: 6,5, assim: Nota – Média = 6,5 – 6,125 = 0,375
4º Bimestre: 8,0, assim: Nota – Média = 8 – 6,125 = 1,875.
5 - Qual a equação de regressão que descreve
a relação entre idade e peso para um bebê do sexo feminino?
Escolha uma:
a.
y = 5 + 0,35x X
b.
y = -5 + 0,35x
c.
y = 5 - 0,35x
d.
y = -5 - 0,35x
e.
Não é possível obter a equação de regressão por não existir correlação entre
idade e peso de um bebê do sexo feminino.
6 - Dois amigos jogam par ou ímpar por 5
vezes. Determine a probabilidade aproximada de sair par 4 vezes.
Escolha uma:
a.
6%.
b.
16%. X
c.
26%.
d.
36%
e.
46%
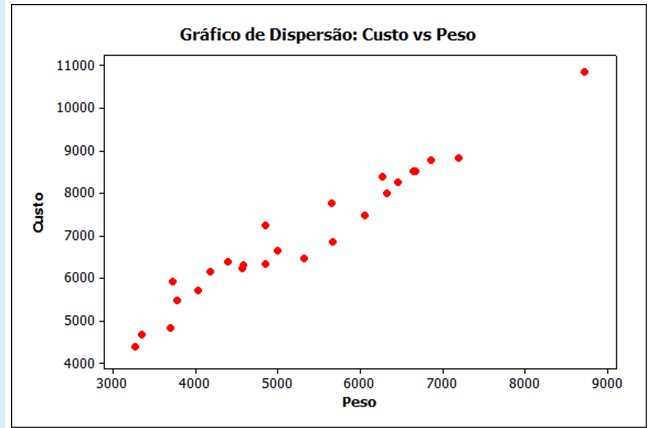
7 - Mediante o gráfico abaixo, analise as
afirmativas:
Fonte: disponível em
<https://www.escolaedti.com.br/entender-correlacao-entre-variaveis/>
I) Existe uma
correlação fraca entre custo e peso.
II) Existe uma
correlação forte entre custo e peso.
III) O gráfico de dispersão
que representa a correlação entre custo e peso é crescente.
É correto o que se afirma em:
Escolha uma:
a.
I, apenas.
b.
I e II, apenas.
c.
I e III, apenas.
d.
II, apenas.
e.
II e III, apenas. X
8 - Uma pesquisa sobre as idades dos
funcionários de cinco empresas foi colocada em uma tabela:
Qual empresa apresenta maior homogeneidade
nas idades de seus funcionários?
Escolha uma:
a.
Empresa A
b.
Empresa B
c.
Empresa C
d.
Empresa D
e.
Empresa E X
Primeiro temos que ter em mente dois
conceitos:
Desvio padrão: Quanto maior é o desvio
padrão, maior é a diferença entre os números que foram usados para fazer o
cálculo.
Homogeneidade: significa algo que apresente
certa semelhança.
De acordo com os dados da tabela, a empresa
que apresentará maior homogeneidade, ou seja, maior semelhança entre as idades
de seus funcionários, será aquela que possui o menor desvio padrão.
No caso, a empresa E é a que mais possui
semelhança entre as idades e a empresa D é a que possui maior diferença entre
elas.
9 - Em um depósito foram obtidos os seguintes
dados para os comprimentos (em metros) de uma amostra de 20 rolos de arame:
Dessa amostra podemos concluir que a
distribuição:
Escolha uma:
a.
é simétrica.
b.
tem assimetria positiva.
c.
tem assimetria negativa. X
d.
é parte assimétrica positiva e parte simétrica.
e.
é parte assimétrica negativa e parte simétrica.
Em um depósito (...)
O conteúdo está na Unidade 1, pp. 75-78.
A média dos dados é 50,5.
Mediana é 51.
Moda é 51.
Assimetria Negativa: média ≤ mediana ≤ moda
O conteúdo está na Unidade 1, pp. 75-78.
A média dos dados é 50,5.
Mediana é 51.
Moda é 51.
Assimetria Negativa: média ≤ mediana ≤ moda
10 - Sabendo que a probabilidade de acertar o
alvo em um único tiro é de 0,35, determine a probabilidade aproximada de
acertar o alvo 2 vezes.
Escolha uma:
a.
50%.
b.
46%.
c.
34%.
d.
25%.
e.
13%. X
1 - Sobre medidas de assimetria e curtose,
assinale a alternativa correta:
Escolha uma:
a.
Se a moda for maior que a média aritmética em uma distribuição de frequências,
então a distribuição apresenta assimetria à direita.
b.
Se o coeficiente de excesso de curtose for negativo, a distribuição será
leptocúrtica.
c.
A distribuição normal é platicúrtica.
d.
Se a média aritmética for maior que a moda em uma distribuição de frequências,
então a distribuição é assimétrica positiva. X
e.
A média será igual à moda em uma amostra com assimetria positiva
2 - De acordo com a tabela que relaciona o
número de horas trabalhadas por um certo caixa de supermercado, durante uma
semana, e a quantia recebida por ele, determine o coeficiente de correlação
linear aproximado pelo coeficiente de correlação de Pearson.
Escolha uma:
a.
0,8227.
b.
0,8464.
c.
0,8665.
d.
0,8728. X
e.
0,9001
3 - Bruno está participando de um jogo de
tiro ao alvo cujo tabuleiro é igual ao da figura abaixo.
Sabendo que Bruno atirou 2 vezes e acertou
ambos os tiros na parte de cor preta, a probabilidade de ter acertado nos
números 4 e 8 é de:
Escolha uma:
a.
2/3. X
b.
1/3.
c.
2/6.
d.
1/6.
e.
3/2.
4 - Uma entrevista foi feita com 50 alunos do
2º ano do ensino fundamental I. Nela, o aluno poderia escolher, por preferência,
até duas entre as matérias de Inglês, Educação Física e Arte. Sabe-se que:
I. 25 alunos escolheram
Educação Física e Arte;
II. 15 alunos escolheram
Educação Física e Inglês;
III. 20 alunos escolheram Arte e Inglês;
IV. 40 alunos escolheram Inglês;
V. 45 alunos escolheram Educação
Física;
VI. 45 alunos escolheram Arte.
Qual a probabilidade de um aluno,
escolhido ao acaso, preferir somente a matéria de Inglês?
Escolha uma:
a.
5%.
b.
10%. X
c.
15%.
d.
20%.
e.
25%.
Vamos montar um diagrama de venn para a
questão e analisar ele. O diagrama está anexado no final da resolução.
Vamos construir o diagrama:
Temos 3 grupos principais: Inglês (I), Artes
(A) e Educação Física (E).
I - 25 Alunos fazem Educação Física e Artes,
logo 25 alunos pertencem à interseção entre E e A.
II - 15 alunos fazem Educação física e
Inglês, logo 15 alunos pertencem à interseção entre E e I.
III - 20 alunos fazem parte da interseção
entre A e I.
IV - 40 Alunos, no total, fazem parte do
conjunto I. Lá ja temos 15 + 20 = 35 alunos (conforme o diagrama), logo somente
40 - 35 = 5 alunos fazem apenas inglês.
A probabilidade de escolher um aluno que faz
somente inglês é dada por:
P = (número de alunos que fazem somente
inglês)/(número total de alunos)
Substituindo os valores dados no enunciado e
o valor obtido pelo diagrama construído:
P = 5/50 = 0,1 = 10 %
5 - Ao jogar um dado, que possui 6 faces (1,
2, 3, 4, 5, 6) a probabilidade de que a face voltada para cima seja um número
divisível por 3 é de, aproximadamente:
Escolha uma:
a.
33,33%. X
b.
44,44%.
c.
55,55%.
d.
66,66%.
e.
77,77%.
d3:(3, 6) = 2 números
p= 2/6 =1/3 ==> (33,33%) ✓
6 - A professora de Métodos Estatísticos
anotou as idades dos seus 50 alunos e percebeu uma distribuição normal com
média igual a 23 anos e desvio padrão igual a 2,5. Determine o percentual de
alunos entre 21 e 25 anos.
Escolha uma:
a.
28,81%.
b.
14,4%.
c.
57,62%. X
d.
68,26%.
e.
32,13%.
Resposta:
P( 21 ≤ X ≤25)
=P[(21-23)/2,5 ≤ (X-23)/2,5) ≤ (25-23)/2,5]
=P(-0,8 ≤ Z ≤ 0,8]
=ψ(0,8) -ψ(-0,8)
=ψ(0,8) -[1 -ψ(0,8)]
=2*ψ(0,8) -1
=2 * 0,7881 -1 = 0,5762 ou 57,62%
7 - Foram colocados em uma urna 3 bolas
vermelhas e 2 bolas azuis. Qual a probabilidade que Ana tem de retirar, sem
reposição, duas bolas vermelhas?
Escolha uma:
a.
0,7.
b.
0,6.
c.
0,5.
d.
0,4.
e.
0,3. X
Foram colocas em uma urna 3 bolas (...)
Na primeira tentativa: 3/5 = 60% (3 de 5).
Na segunda tentativa: 2/4 = 50%. (2 de 4, porque foi retirado 1)
Assim, para saber a probabilidade das 3 moedas, tem que multiplicar: P1 x P2 = 0,6 x 0,5 = 0,3 ou 30%.
Na primeira tentativa: 3/5 = 60% (3 de 5).
Na segunda tentativa: 2/4 = 50%. (2 de 4, porque foi retirado 1)
Assim, para saber a probabilidade das 3 moedas, tem que multiplicar: P1 x P2 = 0,6 x 0,5 = 0,3 ou 30%.
8 - Vendo o empenho de seu aluno, o professor
prometeu aumentar na média de sua nota (6,1) o equivalente ao desvio padrão das
mesmas. Sabendo que as notas apresentaram uma variância de 2,25, o aluno
concluiu a disciplina de Matemática com a média:
Escolha uma:
a.
6,1.
b.
7,2.
c.
7,4.
d.
7,6. X
e.
7,8.
9 - Depois de calcular os desvios em relação
à média das notas, um aluno obteve os seguintes valores: -1,875, -0,125, 0,375
e 2,25. A variância da população dessas notas é:
Escolha uma:
a.
2,18. X
b.
1,16.
c.
1,35.
d.
2,73.
e.
1,63.
Depois de calcular (...)
Basta aplicar a fórmula da Variância:
S2=∑ (X1 - )2
________________
N
S2= (3,5156 + 0,01562 + 0,1406 + 5,0625)
4
S2 = 8,7343 / 4
S2 = 2,18.
Basta aplicar a fórmula da Variância:
S2=∑ (X1 - )2
________________
N
S2= (3,5156 + 0,01562 + 0,1406 + 5,0625)
4
S2 = 8,7343 / 4
S2 = 2,18.
10 - No lançamento de 3 moedas honestas, a
probabilidade de se obter 3 caras é igual a:
Escolha uma:
a.
0,5
b.
0,25
c.
0,125 X
d.
0,062
e.
0,03
Resposta:
1/2 ×1/2 ×1/2 = 1/8 = 0,125
1 - Associe as duas colunas, relacionando
cada variável à sua classificação:
A sequência correta dessa associação é:
Escolha uma:
a.
(2), (3), (1), (2), (1).
b.
(1), (3), (2), (3), (1). X
c.
(1), (2), (1), (3), (2).
d.
(3), (1), (3), (2), (2)
e.
(1), (3), (2), (2), (1).
2 - Observe a tabela de distribuição de
frequências de salários dos funcionários de uma empresa:
Na tabela estão faltando quatro valores (um
de frequência absoluta, outro de frequência relativa e dois valores de
frequência acumulada). Esses valores são, respectivamente:
Escolha uma:
a.
5; 30%; 90%; 100%. X
b.
10; 60%; 30%; 100%.
c.
15; 30%; 90%; 10%.
d.
5; 60%; 30%; 10%.
e.
15; 30%; 90%; 100%.
3 - Após o término de seu expediente, Márcia
fechou seu caixa, contou o número de notas de cada valor e colocou em uma tabela:
Ela prometeu à sua filha a nota que fosse a
mediana de todas elas. A menina recebeu:
Escolha uma:
a.
R$ 5,00.
b.
R$ 10,00. X
c.
R$ 20,00.
d.
R$ 50,00.
e.
R$ 100,00.
4 - Em agosto de 2018, o “ESTADÃO” publicou a
pesquisa IBOPE para presidência do Brasil:
Determine o candidato que possui a
porcentagem mediana (considere a ordem alfabética para candidatos com mesma
porcentagem):
Escolha uma:
a.
Guilherme Boulos.
b.
Álvaro Dias.
c.
Vera. X
d.
Henrique Meirelles.
e.
João Amoedo.
15.
Em agosto de 2018, o Estadão (...)
O primeiro passo é colocar os 13 dados em rol crescente (lembre-se de colocar os candidatos que possuem a mesma porcentagem em ordem alfabética).
Cabo Daciolo; Eymael; Guilherme Boulos; Henrique Meirelles; João Amoedo; João Goulart Filho; Vera; Álvaro Dias; Fernando Haddad; Geraldo Alckmin; Ciro Gomes; Marina Silva; Jair Bolsonaro;
Considerando que existem 13 posições, a mediana será 7., assim, quem ocupa a 7ª posição é a VERA.
5 - Observe a tabela de alturas de uma
amostra de 40 pacientes de um médico clínico geral. O paciente com estatura
igual à 1,65 encontra-se:
Escolha uma:
a.
Na classe mediana da tabela.
b.
Na classe modal da tabela.
c.
No terceiro quartil da tabela X
d.
No quinto percentil da tabela.
e.
No segundo decil da tabela.
Observe a tabela de alturas..
Aqui, o paciente com 1,65 está no intervalo: 165 |------ 170, cuja frequência acumulada é 32. Considerando que o total de pacientes é 40, e 32 correspondem a 75% dos dados (32 / 40), a altura 1,65 está no terceiro quartil da tabela (75% dos dados).
6 - Observe o gráfico abaixo:
Fonte: disponível em
<https://sites.google.com/site/marcosfs2006/histograma>.
Fazendo uma estimativa para as frequências
absolutas, podemos afirmar que:
Escolha uma:
a.
Este histograma não possui mediana.
b.
Este histograma não possui moda.
c.
A classe modal está no seguinte intervalo: 1,0 a 1,5. X
d.
A classe mediana é oposta à classe modal.
e.
Não se pode calcular as classes mediana e modal por meio de histogramas.
7 - 1) O histograma é
um diagrama de __________ e o polígono de frequências tem uma configuração
_________.
As palavras que completam corretamente a
frase acima são, respectivamente:
Escolha uma:
a.
Barras; simples.
b.
Colunas; linear. X
c.
Barras; linear.
d.
Colunas; simples.
e.
Linhas; simples.
8 - A tabela que melhor representa o seguinte
polígono de frequências é:
Fonte: disponível em <
http://portefoliodemacsbyrodrigo.blogspot.com/2013/03/710-poligonos-de-frequencias-para-dados.html
>
Escolha uma:
a.
X
|
Temperatura
|
Frequência Absoluta
|
|
12 |------ 17
|
2
|
|
17 |------ 22
|
8
|
|
22 |------ 27
|
1
|
|
TOTAL
|
11
|
b.
|
Temperatura
|
Frequência Absoluta
|
|
14,5
|
2
|
|
19,5
|
8
|
|
24,5
|
1
|
|
TOTAL
|
11
|
c.
|
Temperatura
|
Frequência Absoluta
|
|
9,5 |------ 14,5
|
2
|
|
14,5 |------ 19,5
|
8
|
|
19,5 |------ 24,5
|
1
|
|
TOTAL
|
11
|
d.
|
Temperatura
|
Frequência Absoluta
|
|
14,5
|
2
|
|
19,5
|
6
|
|
24,5
|
7
|
|
TOTAL
|
15
|
e.
|
Temperatura
|
Frequência Absoluta
|
|
9,5 |------ 14,5
|
2
|
|
14,5 |------ 19,5
|
6
|
|
19,5 |------ 24,5
|
7
|
|
TOTAL
|
15
|
9 - Determine o salário médio aproximado dos
funcionários da empresa K:
Escolha uma:
a.
R$ 1056,20.
b.
R$ 1250,00.
c.
R$ 1568,18. X
d.
R$ 1759,49.
e.
R$ 2300,00.
Determine o salário aproximado (...)
O primeiro passo para aplicar a fórmula é acrescentar 2 colunas na tabela:
Na primeira coluna adicional (você pode chamar de X), será para relacionar os pontos médios das faixas salariais. Assim ela ficará da seguinte maneira:
1ª linha: 1000 + 1500 = 2500 / 2 = 1.2502ª linha: 1500 + 2000 = 3500 / 2 = 1.750
3ª linha: 2000 + 2500 = 4500 / 2 = 2.250
Na segunda coluna, você irá multiplicar cada Frequência pelo Ponto Médio (que foi a primeira coluna adicionada), vai ficar da seguinte maneira:
1ª linha: 30 x 1.250 = 37.5002ª linha: 15 x 1.750 = 26.250
3ª linha: 10 x 2.250 = 22.500
(some tudo) = 86.250
Agora, aplique a fórmula da Média dos Dados Agrupados: (total da soma das médias dos dados agrupados) (dividido por) (frequência total)
Média = 86.250 / 55Média dos Salários = R$ 1.568,18.
10 - Uma nutricionista deseja saber a média
de pesos dos seus pacientes. Considerando a tabela abaixo, essa média será de:
Escolha uma:
a.
92,7.
b.
85,7.
c.
76,7.
d.
71,7. X
e.
66,7.
2 - João e Duda fizeram uma aposta. Ele disse
que conseguiria jogar dois dados simultaneamente e, ao somar os números das
faces voltadas para cima, obter o número 7. Cada dado possui 6 faces (1, 2, 3,
4, 5, 6).
Considerando o enunciado, assinale a
alternativa correta:
Escolha uma:
a.
50% de chance de ganhar a aposta.
b.
25% de chance de ganhar a aposta.
c.
aproximadamente 10% de chance de perder a aposta.
d.
15% de chance de perder a aposta.
e.
aproximadamente 17% de chance de ganhar a aposta X
3 - Examinando um conjunto de dados,
observa-se que a distribuição de frequências de notas dos alunos de uma turma é
assimétrica à esquerda. Com base nessa afirmação, é correto afirmar que:
Escolha uma:
a.
A maior parte dos alunos está com nota abaixo da média da turma.
b.
A nota modal é maior que a nota média da turma. X
c.
A maior parte dos alunos está com nota acima da média da turma.
d.
A média da turma é maior que a nota modal.
e.
A média da turma é igual à nota modal.
Examinando um conjunto de dados (...)
O conteúdo está na Unidade 1, pp. 75-81.
Assimétrica negativa se média ≤ mediana ≤ moda ou As < 0.
O conteúdo está na Unidade 1, pp. 75-81.
Assimétrica negativa se média ≤ mediana ≤ moda ou As < 0.
O lado mais longo do polígono de frequência (cauda da distribuição) está à esquerda do centro.
Assim, observe que a moda é maior que a média.