Blog Educacional/LANA

[OFICINA DE MATEMÁTICA – CICLO I]

Esta oficina de matemática tem como objetivo apresentar as professoras do Ciclo I, alguns materiais didáticos disponíveis nesta Unidade Educacional assim como conversarmos sobre a oportunidade de seus usos com os alunos, visando maior riqueza que os mesmos nos oferecem no trabalho com os conteúdos desta disciplina.

Sumário

1 - COMO USAR BEM O MATERIAL CONCRETO EM SALA DE AULA

• Planeje seu trabalho. Determine os conteúdos a serem desenvolvidos durante o ano e como eles podem ser aprendidos com o uso de material concreto.

• Utilize o mesmo material para diferentes funções e em diferentes níveis, dependendo do objetivo. É interessante mostrar essa versatilidade aos estudantes.

• Permita que a turma explore bem o material antes de iniciar a atividade - o ideal é que cada aluno tenha o seu. Se isso não for possível, forme duplas.

Depois explique como ele será usado.

• Apresente uma situação-problema significativa para o aluno: ele precisa ter estímulo para resolvê-la.

• Observe as crianças: para perceber o raciocínio de cada uma, ajude-as a pensar sobre o que estão fazendo.

• Para saber se o estudante está de fato aprendendo, peça o registro das atividades realizadas com o material na forma de desenho ou na linguagem matemática.

• A turma fica mais agitada e conversa mais que o normal durante esse tipo de atividade. Interprete essa "bagunça saudável" como um momento de troca.

2 - MATERIAL DOURADO

O Material Dourado Montessori destina-se a atividades que auxiliam o ensino e a aprendizagem do sistema de numeração decimal-posicional e dos métodos para efetuar as operações fundamentais (ou seja, os algoritmos).

No ensino tradicional, as crianças acabam "dominando" os algoritmos a partir de treinos cansativos, mas sem conseguirem compreender o que fazem.

Com o Material Dourado a situação é outra: as relações numéricas abstratas passam a ter uma imagem concreta, facilitando a compreensão.

Obtém-se, então, além da compreensão dos algoritmos, um notável desenvolvimento do raciocínio e um aprendizado bem mais agradável.

O Material Dourado faz parte de um conjunto de materiais idealizados pela médica e educadora italiana Maria Montessori.

2.1 – QUEM FOI MARIA MONTESSORI

Nos anos iniciais deste século, Maria Montessori dedicou-se à educação de crianças excepcionais, que, graças à sua orientação, rivalizavam nos exames de fim de ano com as crianças normais das escolas públicas de Roma. Esse fato levou Maria Montessori a analisar os métodos de ensino da época e a propor mudanças compatíveis com sua filosofia de educação.

Segundo Maria Montessori, a criança tem necessidade de mover-se com liberdade dentro de certos limites, desenvolvendo sua criatividade no enfrentamento pessoal com experiências e materiais. Um desses materiais era o chamado material das contas que, posteriormente, deu origem ao conhecido Material Dourado Montessori.

2.2 – O MATERIAL DOURADO MONTESSORI

O material Dourado ou Montessori é constituído por cubinhos, barras, placas e cubão, que representam:

Observe que o cubo é formado por 10 placas, que a placa é formada por 10 barras e a barra é formada por 10 cubinhos. Este material baseia-se em regras do nosso sistema de numeração.

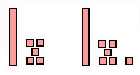
Veja como representamos, com ele, o número 265:

Este material pedagógico, confeccionado em madeira, costuma ser comercializado com o nome de material dourado. Você pode construir um material semelhante, usando cartolina. Os cubinhos são substituídos por quadradinhos de lado igual a 2 cm, por exemplo. As barrinhas são substituídas por retângulos de 2 cm por 20 cm a as placas são substituídas por quadrados de lado igual a 20 cm.

Embora seja possível representar o milhar, vamos evitá-lo trabalhando com números menores.

Damos a seguir sugestões para o uso do Material Dourado Montessori.

As atividades propostas foram testadas e mostraram-se eficazes desde a primeira até a quinta série. Muitas delas foram concebidas pelos grupos de alunos, recomendando-se que os grupos não tenham mais do que 6 alunos.

O professor, com o conhecimento que tem de seus alunos, saberá em que série cada atividade poderá ser aplicada com melhor rendimento. Várias das atividades podem ser aplicadas em mais de uma série, bastando, para isso, pequenas modificações.

Utilizando o material, o professor notará em seus alunos um significativo avanço de aprendizagem. Em pouco tempo, estará enriquecendo nossas sugestões e criando novas atividades adequadas a seus alunos, explorando assim as inúmeras possibilidades deste notável recurso didático.

2.3- SUGESTÕES DE ATIVIDADES COM MATERIAL DOURADO

2.3.1 - JOGOS LIVRES

Objetivo: tomar contato com o material, de maneira livre, sem regras.

Durante algum tempo, os alunos brincam com o material de forma livre, fazendo construções.

O material dourado é construído de maneira a representar um sistema de agrupamento. Sendo assim, muitas vezes as crianças descobrem sozinhas relações entre as peças. Por exemplo, podemos encontrar alunos que concluem:

- Ah! A barra é formada por 10 cubinhos!

- E a placa é formada por 10 barras!

- Veja, o cubo é formado por 10 placas!

2.3.2 – MONTAGEM

Objetivo: perceber as relações que há entre as peças.

O professor sugere as seguintes montagens:

- uma barra;

- uma placa feita de barras;

- uma placa feita de cubinhos;

- um bloco feito de barras;

- um bloco feito de placas;

O professor estimula os alunos a obterem conclusões com perguntas como estas:

- Quantos cubinhos vão formar uma barra?

- E quantos formarão uma placa?

- Quantas barras preciso para formar uma placa?

Nesta atividade também é possível explorar conceitos geométricos, propondo desafios como estes:

- Vamos ver quem consegue montar um cubo com 8 cubinhos? É possível?

- E com 27? É possível?

2.3.3 – DITADO

Objetivo: relacionar cada grupo de peças ao seu valor numérico.

O professor mostra, um de cada vez, cartões com números. As crianças devem mostrar as peças correspondentes, utilizando a menor quantidade delas.

Variação:

O professor mostra peças, uma de cada vez, e os alunos escrevem a quantidade correspondente.

2.3.4 – FAZENDO TROCAS

Objetivo: compreender as características do sistema decimal.

- fazer agrupamentos de 10 em 10;

- fazer reagrupamentos;

- fazer trocas;

- estimular o cálculo mental.

Para esta atividade, cada grupo deve ter um dado marcado de 4 a 9.

Cada criança do grupo, na sua vez de jogar, lança o dado e retira para si a quantidade de cubinhos correspondente ao número que sair no dado.

Veja bem: o número que sai no dado dá direito a retirar somente cubinhos.

Toda vez que uma criança juntar 10 cubinhos, ela deve trocar os 10 cubinhos por uma barra. E aí ela tem direito de jogar novamente.

Da mesma maneira, quando tiver 10 barrinhas, pode trocar as 10 barrinhas por uma placa e então jogar novamente.

O jogo termina, por exemplo, quando algum aluno consegue formar duas placas.

O professor então pergunta:

- Quem ganhou o jogo?

- Por quê?

Se houver dúvida, fazer as "destrocas".

O objetivo do jogo das trocas é a compreensão dos agrupamentos de dez em dez (dez unidades formam uma dezena, dez dezenas formam uma centena, etc.),

característicos do sistema decimal.

A compreensão dos agrupamentos na base 10 é muito importante para o real entendimento das técnicas operatórias das operações fundamentais.

O fato de a troca ser premiada com o direito de jogar novamente aumenta a atenção da criança no jogo. Ao mesmo tempo, estimula seu cálculo mental. Ela começa a calcular mentalmente quanto falta para juntar 10, ou seja, quanto falta para que ela consiga fazer uma nova troca.

cada placa será destrocada por 10 barras;

cada barra será destrocada por 10 cubinhos.

Variações:

Pode-se jogar com dois dados e o aluno pega tantos cubinhos quanto for a soma dos números que tirar dos dados.

Pode-se utilizar também uma roleta indicando de 1 a 9.

2.3.5 – PREENCHENDO TABELAS

Objetivo: os mesmos das atividades 5.3 e 5.4

- preencher tabelas respeitando o valor posicional;

- fazer comparações de números;

- fazer ordenação de números.

As regras são as mesmas da atividade 4. Na apuração, cada criança escreve em uma tabela a quantidade conseguida.

Olhando a tabela, devem responder perguntas como estas:

- Quem conseguiu a peça de maior valor?

- E de menor valor?

- Quantas barras Lucilia tem a mais que Gláucia?

Olhando a tabela à procura do vencedor, a criança compara os números e percebe o valor posicional de cada algarismo.

Por exemplo: na posição das dezenas, o 2 vale 20; na posição das centenas vale 200.

Ao tentar determinar os demais colocados (segundo, terceiro e quarto lugares) a criança começa a ordenar os números.

2.3.6 – PARTINDO DE CUBINHOS

Objetivo: os mesmos da atividade 5.3, 5.4 e 5.5.

Cada criança recebe certo número de cubinhos para trocar por barras e depois por placas.

A seguir deve escrever na tabela os números correspondentes às quantidades de placas, barras e cubinhos obtidos após as trocas.

Esta atividade torna-se interessante na medida em que se aumenta o número de cubinhos.

2.3.7 – VAMOS FAZER UM TREM?

Objetivo: compreender que o sucessor é o que tem "1 a mais" na seqüência numérica.

O professor combina com os alunos:

- Vamos fazer um trem. O primeiro vagão é um cubinho. O vagão seguinte terá um cubinho a mais que o anterior e assim por diante. O último vagão será formado por duas barras.

Quando as crianças terminarem de montar o trem, recebem papeletas nas quais devem escrever o código de cada vagão.

Esta atividade leva à formação da ideia de sucessor. Fica claro para a criança o "mais um", na seqüência dos números. Ela contribui também para a melhor compreensão do valor posicional dos algarismos na escrita dos números.

2.3.8 – UM TREM ESPECIAL

Objetivo: compreender que o antecessor é o que tem "1 a menos" na seqüência numérica.

O professor combina com os alunos:

- Vamos fazer um trem especial. O primeiro vagão é formado por duas barras (desenha as barras na lousa). O vagão seguinte tem um cubo a menos e assim por diante. O último vagão será um cubinho.

Quando as crianças terminam de montar o trem, recebem papeletas nas quais devem escrever o código de cada vagão.

Esta atividade trabalha a ideia de antecessor. Fica claro para a criança o "menos um" na seqüência dos números. Ela contribui também para uma melhor compreensão do valor posicional dos algarismos na escrita dos números.

2.3.9 – JOGO DOS CARTÕES

Objetivos: compreender o mecanismo do "vai um" nas adições; estimular o cálculo mental.

O professor coloca no centro do grupo alguns cartões virados para baixo. Nestes cartões estão escritos números entre 50 e 70.

1º sorteio: Um alunos do grupo sorteia um cartão. Os demais devem pegar as peças correspondentes ao número sorteado.

Em seguida, um representante do grupo vai à lousa e registra em uma tabela os números correspondentes às quantidades de peças.

2º sorteio: Um outro aluno sorteia um segundo cartão. Os demais devem pegar as peças correspondentes a esse segundo número sorteado.

Em seguida, o representante do grupo vai à tabela registrar a nova quantidade.

Nesse ponto, juntam-se as duas quantidades de peças, fazem-se as trocas e novamente completa-se a tabela.

Ela pode ficar assim:

Isto encerra uma rodada e vence o grupo que tiver conseguido maior total.

Depois são feitas mais algumas rodadas e o vencedor do dia é o grupo que mais rodadas venceu.

Os números dos cartões podem ser outros. Por exemplo, números entre 10 e 30, na primeira série; entre 145 e 165, na segunda série.

Depois que os alunos estiverem realizando as trocas e os registros com desenvoltura, o professor pode apresentar a técnica do "vai um" a partir de uma adição como, por exemplo, 15 + 16.

Observe que somar 15 com 16 corresponde a juntar estes conjuntos de peças.

Fazendo as trocas necessárias,

Compare, agora, a operação:

com o material

com os números

Ao aplicar o "vai um", o professor pode concretizar cada passagem do cálculo usando o material ou desenhos do material, como os que mostramos.

O "vai um" também pode indicar a troca de 10 dezenas por uma centena, ou 10 centenas por 1 milhar, etc.

Veja um exemplo:

No exemplo que acabamos de ver, o "vai um" indicou a troca de 10 dezenas por uma centena.

É importante que a criança perceba a relação entre sua ação com o material e os passos efetuados na operação.

2.3.10 – O JOGO DE RETIRAR

Objetivos: compreender o mecanismo do "empresta um" nas subtrações com recurso; estimular o cálculo mental.

Esta atividade pode ser realizada como um jogo de várias rodadas. Em cada rodada, os grupos sorteiam um cartão e uma papeleta. No cartão há um número e eles devem pegar as peças correspondentes a essa quantia. Na papeleta há uma ordem que indica quanto devem tirar da quantidade que têm.

Por exemplo: cartão com número 41 e papeleta com a ordem: TIRE 28.

Vence a rodada o grupo que ficar com as peças que representam o menor número. Vence o jogo o grupo que ganhar mais rodadas.

É importante que, primeiro, a criança faça várias atividades do tipo: "retire um tanto", só com o material. Depois que ela dominar o processo de "destroca", pode-se propor que registre o que acontece no jogo em uma tabela na lousa.

Isto irá proporcionar melhor entendimento do "empresta um" na subtração com recurso. Quando o professor apresentar essa técnica, poderá concretizar os passos do cálculo com auxílio do material ou desenhos do material.

O "empresta um" também pode indicar a "destroca" de uma centena por 10 dezenas ou um milhar por 10 centenas, etc. Veja o jogo seguinte:

2.3.11 – DESTROCA

Objetivos: os mesmos da atividade 10.

Cada grupo de alunos recebe um dado marcado de 4 a 9 e uma placa.

Quando o jogador começa, todos os participantes têm à sua frente uma placa.

Cada criança, na sua vez de jogar, lança o dado e faz as "destrocas" para retirar a quantidade de cubinhos correspondente ao número que sair no dado. Veja bem: esse número dá direito a retirar somente cubinhos.

Na quarta rodada, vence quem ficar com as peças que representam o menor número.

Exemplo: Suponha que um aluno tenha tirado 7 no dado. Primeiro ele troca uma placa por 10 barras e uma barra por 10 cubinhos:

Depois, retira 7 cubinhos:

Salientamos novamente a importância de se proporem várias atividades como essa, utilizando, de início, só o material. Quando o processo de "destroca" estiver dominado, pode-se propor que as crianças façam as subtrações envolvidas também com números.

3 – MATERIAL CUISENAIRE

O Material Cuisenaire tem mais de 50 anos de utilização em todo o mundo.

Foi criado pelo professor belga Georges Cuisenaire Hottelet (1891-1980) depois de ter observado o desespero de um aluno, numa das suas aulas.

Decidiu criar um material que ajudasse no ensino dos conceitos básicos da Matemática tais como: explorar seqüência numérica; frações (o aluno identifica as relações entre a parte e o todo); coordenação motora; memória; análise-síntese;

constância de percepção de forma, tamanho e cores.

Então cortou algumas réguas de madeira em 10 tamanhos diferentes e pintou cada peça de uma cor tendo assim surgido a Escala de Cuisenaire.

Durante 23 anos, Cuisenaire estudou e experimentou o material que criara na aldeia belga de Thuin.

Só 23 anos depois da sua criação (a partir de um encontro com outro professor – o egípcio Caleb Gattegno), é que o seu uso se difundiu com enorme êxito. O egípcio, radicado na Inglaterra, passou a divulgar o trabalho de Cuisenaire – a quem chamava de Senhor Barrinhas.

Levou apenas 13 anos para passar a ser conhecido nas escolas de quase todo o mundo.

Feito originalmente de madeira, o Cuisenaire é constituído por modelos de prismas quadrangulares com alturas múltiplas da do cubo – representante do número 1 – em 10 cores diferentes e 10 alturas proporcionais.

COR	NÚMERO REPRESENTADO
Branco (ou cor de madeira)	1
Vermelho	2
Verde-claro	3
Rosa (ou lilás)	4
Amarelo	5
Verde-escuro	6
Preto	7
Castanho	8
Azul	9
Cor de laranja (ou cor de madeira)	10

3.1- SUGESTÕES DE ATIVIDADES COM MATERIAL CUISENAIRE

3.1.1 - PINTAR DA COR CORRESPONDENTE AS BARRAS QUE FALTAM PINTAR E RESPONDER:

Pega numa barra de cada cor.

Colocar na mesa essas barras pela ordem de tamanho, da menor até a maior.

• De que cor é a barra menor?

• De que cor é a barra maior?

• De que cor são as barras menores que a amarela?

• Qual a barra imediatamente menor que a amarela?

• Quais são as barras maiores que a preta?

• Qual a barra que é imediatamente maior que a preta?

• Qual a barra que está entre a verde-escuro e a castanha?

• Quais são as barras que estão entre a amarela e a verde-escura?

• Quantas barras brancas são necessárias para formar uma barra do mesmo tamanho que a vermelha?

• Quantas barras brancas são necessárias para formar uma barra do mesmo tamanho que a verde-clara?

• Quantas barras brancas são necessárias para formar uma barra do mesmo tamanho que a cor-de-rosa?

• Quantas barras brancas são necessárias para formar uma barra do mesmo tamanho que a amarela?

3.1.2 - CONSIDERA A BARRA BRANCA COMO UNIDADE DE MEDIDA (A BARRA BRANCA VALE 1).

Quanto vale a barra vermelha?

Quanto vale a barra amarela?

Quanto vale a barra castanha?

3.1.3 – REPRESENTAR NÚMEROS

Construir o número 7 com duas barras.

Sem repetir barras da mesma cor, de quantas maneiras diferentes podes representar o número 9. Representa-as na folha.

Forma o número 8, só com barras vermelhas e brancas.

Quantas soluções encontrou? ____________________

3.1.4 – COBRIR SUPERFÍCIES

Com o material Cuisenaire cobre a superfície ocupada pela girafa da figura.

3.1.5 - JOGOS DE INICIAÇÃO À ADIÇÃO

Amarela + Verde-clara = Castanha”

3.1.6- INÍCIO DO ESTUDO E COMPARAÇÃO DE “PARTES DE”

A mãe da Joana e do Pedro comprou-lhes dois chocolates iguais num supermercado.

No dia seguinte, ambos repararam que cada chocolate podia dividir-se em dez pedacinhos iguais. Enquanto que o Pedro decidiu comer de manhã sete desses dez pedacinhos, guardando os restantes três para depois do almoço, a Joana decidiu guardar a maior parte do chocolate para essa altura, comendo somente de manhã, três dos dez pedacinhos do seu chocolate.

Que parte do chocolate comeu o Pedro de manhã?

b) Que parte do chocolate comeu a Joana de manhã?

c) Quem comeu mais chocolate nessa parte do dia, o Pedro ou a Joana?

d) A quem sobrou mais chocolate para comer da parte de tarde?

3.1.7 - INICIAÇÃO AO ESTUDO DA PROPRIEDADE COMUTATIVA DA ADIÇÃO

a) Quem comeu mais chocolate no final desse dia?

3.1.8 - INICIAÇÃO AO ESTUDO DAS FRAÇÕES EQUIVALENTES

Numa Segunda-feira, Ricardo tentava explicar ao seu melhor amigo,Rui, um problema que se lhe tinha colocado à hora de almoço do dia anterior, a propósito de um bolo que comeram nesse dia. Então, contava Ricardo:

A minha mãe Irene, ao pegar na faca para partir o bolo disse que iria ser a pessoa que iria comer mais bolo, pois, das doze fatias que o compunham, pretendia comer metade.

O meu pai Artur, interrompeu-a dizendo que seria ele o que iria comer mais, uma vez que pretendia comer a terça parte do bolo.

A minha irmã Mónica, como é muito gulosa disse que ela é que iria comer mais fatias, pois iria comer quatro fatias.

Depois de muito pensar, disse-lhes que seria eu quem comeria mais bolo, pois pretendia comer seis fatias.

Você consegue adivinhar, Rui, quem de nós comeu mais fatias inteiras do bolo?

Analisando o esquema anterior e, tendo em conta o tamanho do bolo, alguma dúvida ainda a haver estaria entre o que a sua mãe comeu e aquilo que você comeu. Por um lado a sua mãe disse que dividia o bolo em duas partes iguais e comia uma delas. Por outro lado, você comia seis das doze fatias. Tenho necessidade de comparar essas duas quantidades:

Posso concluir que se assim fosse ambos teriam comido igual quantidade de bolo, pois seria igual dizer que comiam metade do bolo ou seis das doze fatias desse bolo.

Não acredito é que isso tenha ocorrido, pois o seu pai e a sua irmã não comeriam nada desse bolo! Já agora deixa-me perguntar-te quem pretendia comer mais bolo, o seu pai ou a sua irmã?

Tal como você concluiu antes, também eu posso concluir que, se assim fosse, ambos teriam comido igual quantidade de bolo, pois seria igual dizer que comiam a terça parte do bolo ou quatro das doze fatias desse bolo.

3.1.9 - JOGOS ENVOLVENDO OPERAÇÕES COM FRAÇÕES

Estando-se discutindo sobre as contribuições que cada membro da família deveria dar para pagar o bolo, o pai referiu que contribuiria para pagar um quarto do bolo e a Mónica pagaria a sexta parte. Se o Ricardo pagasse o dobro da quantia paga pela irmã, que parte do custo do bolo ficaria para a mãe pagar?